Component-based reduced basis for parametrized symmetric eigenproblems

Sylvain Vallaghé; Phuong Huynh; David J Knezevic; Loi Nguyen; Anthony T Patera

doi:10.1186/s40323-015-0021-0

Advanced Modeling and Simulation in Engineering Sciences Cover Image

Research Article

Open Access

Component-based reduced basis for parametrized symmetric eigenproblems

Sylvain Vallaghé^{1, 4}Email author,
Phuong Huynh^{1, 3},
David J Knezevic^{1, 2, 3},
Loi Nguyen³ and
Anthony T Patera¹

Advanced Modeling and Simulation in Engineering Sciences20152:7

https://doi.org/10.1186/s40323-015-0021-0

Received: 17 October 2014

Accepted: 14 January 2015

Published: 23 May 2015

Abstract

Background

A component-based approach is introduced for fast and flexible solution of parameter-dependent symmetric eigenproblems.

Methods

Considering a generalized eigenproblem with symmetric stiffness and mass operators, we start by introducing a “ σ-shifted” eigenproblem where the left hand side operator corresponds to an equilibrium between the stiffness operator and a weighted mass operator, with weight-parameter σ>0. Assuming that σ=λ _n>0, the nth real positive eigenvalue of the original eigenproblem, then the shifted eigenproblem reduces to the solution of a homogeneous linear problem. In this context, we can apply the static condensation reduced basis element (SCRBE) method, a domain synthesis approach with reduced basis (RB) approximation at the intradomain level to populate a Schur complement at the interdomain level. In the Offline stage, for a library of archetype subdomains we train RB spaces for a family of linear problems; these linear problems correspond to various equilibriums between the stiffness operator and the weighted mass operator. In the Online stage we assemble instantiated subdomains and perform static condensation to obtain the “ σ-shifted” eigenproblem for the full system. We then perform a direct search to find the values of σ that yield singular systems, corresponding to the eigenvalues of the original eigenproblem.

Results

We provide eigenvalue a posteriori error estimators and we present various numerical results to demonstrate the accuracy, flexibility and computational efficiency of our approach.

Conclusions

We are able to obtain large speed and memory improvements compared to a classical Finite Element Method (FEM), making our method very suitable for large models commonly considered in an engineering context.

Keywords

Eigenproblems Domain synthesis Reduced basis A Posteriori error estimation

Background

In structural analysis, eigenvalue computation is necessary to find the periods at which a structure will naturally resonate. This is especially important for instance in building engineering, to make sure that a building’s natural frequency does not match the frequency of expected earthquakes. In the case of resonance, a building can endure large deformations and important structural damage, and possibly collapse. The same considerations apply to automobile and truck frames, where it is important to avoid resonance with the engine frequencies. Eigenproblems also appear when considering wind loads, rotating machinery, aerospace structures; in some cases it is also desirable to design a structure for resonance, like certain microelectromechanical systems.

With improvement in computer architecture and algorithmic methods, it is now possible to tackle large-scale eigenvalue problems with millions of degrees of freedom; however the computations are still heavy enough to preclude usage in a many-query context, such as interactive design of a parameter-dependent system. In this paper, we present an approach for fast solution of eigenproblems on large systems that present a component-based structure – such as building structures.

For the numerical solutions of partial differential equations (PDE) in component-based systems, several computational methods have been introduced to take advantage of the component-based structure. The main idea of these methods is to perform domain decomposition, and to use a common model order reduction for each family of similar components. The first and classical approach is the component mode synthesis (CMS) as introduced in [1,2]: it uses the eigenmodes of local constrained eigenvalue problems for the approximation within the interior of the component and static condensation to arrive at a (Schur complement) system associated with the coupling modes on the interfaces or ports. One drawback of the CMS approach is the rather slow convergence of eigenmodal expansions. In contrast the reduced basis element (RBE) method [3] employs a reduced basis expansion [4] within each component or subdomain and Lagrange multipliers to couple the local bases and hence compute a global solution of the considered parameter dependent partial differential equation for each admissible parameter. The RBE method thus profits from the fact that RB approximations yield a rapid and in many cases exponential convergence [5].

A combination of RB methods and domain decomposition approaches has for instance also been considered in [6,7]. Similarly RB methods have been employed in the framework of a multi-scale finite element method to construct local reduced spaces for the approximation of fine-scale features on the coarse grid elements in [8,9], where the latter corresponds to the “components” in the RBE method.

In [10], a static condensation RBE (SCRBE) approach is developed for elliptic problems. It brings together ideas of CMS and RBE by considering standard static condensation at the interdomain level and then RB approximation at the intradomain level. In an Offline stage performed once, the RB space for a particular component is designed to reflect all possible function variations on the component interfaces (which we shall denote “ports”); components are thus completely interchangeable and interoperable. During the Online stage, any system can be assembled from multiple instantiations of components from a predefined library; we can then compute the system solution for different values of the component parameters in a prescribed parameter domain. The Online stage of the SCRBE is much more flexible than both the Online stage for the standard RB method, in which the system is already assembled and only parametric variations are permitted, and the Online stage of the classical (non-static-condensation) RBE method, in which the RB intradomain spaces already reflect anticipated connectivity.

In this paper, we present an extension of the SCRBE to eigenproblems. The new aspects are the following. First, the SCRBE normally takes advantage of linearity, which is lost when considering eigenproblems. Hence we begin by reformulating the eigenproblem using a shift σ of the spectrum in order to recover a linear problem. Finding the eigenvalues is then performed at a higher level: using a direct search method, we find the values of the shift σ that correspond to singular systems. Second, we provide a posteriori error estimators of the eigenvalues, not only with respect to RB approximations but also in the context of port reduction.

In the context of CMS approaches for eigenproblems, out method provides some important features: treatment of parameter-dependent systems (as explained above), optimal convergence, and port reduction. The classical CMS only achieves a polynomial convergence rate [11,12] with respect to the number of eigenmodes used at the intradomain level. This can be improved to an infinite convergence rate by using overlapping components [12], but at the expense of losing simplicity and flexibility of component connections. Our method somehow provides an optimal trade-off since it retains the interface treatment of classical CMS – allowing flexibility of component connections – while achieving an exponential convergence rate with respect to the size of RB spaces at the intradomain level.

We also provide port reduction so as to increase even more the speed up. Recent CMS contributions consider several port economizations (or interface reduction strategies): an eigenmode expansion (with subsequent truncation) for the port degrees of freedom is proposed in [11,13]; an adaptive port reduction procedure based on a posteriori error estimators for the port reduction is proposed in [14]; and an alternative port reduction approach, with a different bubble function approximation space, is proposed for time-dependent problems in [15]. We can not directly apply CMS port reduction concepts in the parameter-dependent context, as the chosen port modes must be able to provide a good representation of the solution for any value of the parameters. In this paper, we adapt to parameter-dependent eigenproblems a port approximation and a posteriori error bound framework introduced in [16] for parameter-dependent linear elliptic problems.

The paper proceeds as follows. In Section ‘Formulation’, we present the general eigenproblem and its shifted formulation; we then describe the static condensation procedure. In Section ‘Reduced basis static condensation system’, we add reduced basis approximations and develop a posteriori error estimators for the eigenvalues with respect to the corresponding values obtained by the “truth” static condensation of Section ‘Formulation’. In section ‘Port reduction’, we introduce port reduction and provide as well a posteriori error estimators for the eigenvalues. In Section ‘Computational aspects’, we give an overview of the computational aspects of the method. This section somehow brings together all of the previous sections in a compact presentation, and we suggest the reader to often go back to Section ‘Computational aspects’ in order to get a higher level description of the method. Finally, in Section ‘Results and discussion’, we present numerical results to illustrate the computational efficiency of the approach. We first consider simple bridge structures for which we examine the error estimates. We finish with an industrial scale example to show the method’s potential to tackle large systems.

Methods

Formulation

Problem statement

We suppose that we are given an open domain $\Omega \subset \mathbb {R}^{d}$, d=1,2 or 3, with boundary ∂ Ω. We then let X denote the Hilbert space

$$X \equiv \left\{ v \in H^{1}(\Omega) \colon v|_{\partial\Omega_{D}} = 0 \right\} \, $$

where ∂ Ω _D⊂∂ Ω is the portion of the boundary on which we enforce homogeneous Dirichlet boundary conditions. We suppose that X is endowed with an inner product (·,·)_X and induced norm ∥·∥_X. Recall that for any domain

in $\mathbb {R}^{d}$,

$$\begin{array}{*{20}l} H^{1} (\mathcal{O})& \equiv \left\{ v \in L^{2} (\mathcal{O}) \colon \nabla v \in (L^{2} (\mathcal{O}))^{d} \right\},\\ \text{where}\ L^{2} (\mathcal{O}) &\equiv \left\{ v\ \text{measurable over}\ \mathcal{O} \colon \int_{\mathcal{O}} v^{2}\ \text{finite}\, \right\}. \end{array} $$

Furthermore, let Y≡L ²(Ω).

We now introduce an abstract formulation for our eigenvalue problem. For any $\mu \in \mathcal {D}$, let $a(\cdot,\cdot ;\mu):X\times X\rightarrow \mathbb {R}$, and $m_{}(\cdot,\cdot ;\mu):X_{}\times X_{}\rightarrow \mathbb {R}$ denote continuous, coercive, symmetric bilinear form with respect to Xand Y, respectively. We suppose that $X^{\mathcal {N}} \subset X$ is a finite element space of dimension

. Given a parameter $\mu \in \mathcal {D} \subset \mathbb {R}^{P}$, where

is our parameter domain of dimension P, we find the set of eigenvalues and eigenvectors (λ(μ),u(μ)), where $\lambda (\mu) \in \mathbb {R}_{> 0}$ and $u(\mu) \in X^{\mathcal {N}}$ satisfy

$$\begin{array}{@{}rcl@{}} a(u(\mu),v;\mu) &=& \lambda(\mu)m(u(\mu),v;\mu), \quad \forall v \in X^{\mathcal{N}}, \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} m(u(\mu),u(\mu);\mu) &=& 1. \end{array} $$

(2)

We assume that the eigenvalues λ _n(μ) are sorted such that $0 < \lambda _{1}(\mu) \leq \lambda _{2}(\mu) \ldots \leq \lambda _{\mathcal {N}}(\mu)$, and to each eigenvalue λ _n(μ) we associate a corresponding eigenvector u _n(μ). We can have multiplicities greater than one and hence we can have equal successive eigenvalues λ _n(μ)=⋯=λ _n+k(μ) but each associated to linearly independent eigenvectors.

The parametric dependence of the problem usually takes the form of variable PDE coefficients or variable geometry. For instance, in linear elasticity, the vector μ can contain the different Young’s modulus values of different subdomains, as well as the parameters of some mapping function describing the geometrical variability.

We now define a surrogate eigenvalue problem that will be convenient for subsequent developments. For a given “shift factor” $\sigma \in \mathbb {R}_{\geq 0}$, we modify (1), (2) such that for any $\mu \in \mathcal {D}$, we find $\tau (\mu,\sigma) \in \mathbb {R}$ and $\chi (\mu,\sigma) \in X^{\mathcal {N}}$ that satisfy

$$\begin{array}{@{}rcl@{}} \mathcal{B}(\chi(\mu,\sigma),v;\mu;\sigma) &=& \tau(\mu,\sigma)a(\chi(\mu,\sigma),v;\mu), \quad \forall v \in X^{\mathcal{N}}, \quad \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} a(\chi(\mu,\sigma),\chi(\mu,\sigma);\mu) &=& 1. \end{array} $$

(4)

Here

$$ \mathcal{B}(w,v;\mu;\sigma) \equiv a(w,v;\mu) -\sigma m(w,v;\mu) $$

(5)

is our “shifted” bilinear form. Note that we change the bilinear form on the right hand side from m(·,·) to a(·,·), which corresponds to a different norm. This choice is motivated by error estimation, presented later in the paper, as it permits to derive relative error estimates for the eigenvalue λ _n(μ).

We also sort the set of eigenvalues such that $\tau _{1}(\mu,\sigma) \leq \tau _{2}(\mu,\sigma) \ldots \leq \tau _{\mathcal {N}}(\mu,\sigma)$ – note that due to the shift the first eigenvalues can now be negative. It is clear that $\chi _{n}(\mu,\sigma) = \frac {1}{\sqrt {\lambda _{n}(\mu)}}u_{n}(\mu)$ for any $\sigma \in \mathbb {R}$, so we shall henceforth write χ _n(μ). Also

$$ \tau_{n}(\mu,\sigma) = \frac{\lambda_{n}(\mu) - \sigma}{\lambda_{n}(\mu)}, $$

(6)

so that

$$\begin{array}{@{}rcl@{}} \tau_{n}(\mu,\sigma) >0, && \text{if}\enspace 0 \leq \sigma < \lambda_{n}(\mu), \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} \tau_{n}(\mu,\sigma) =0, && \text{if}\enspace \sigma = \lambda_{n}(\mu), \end{array} $$

(8)

$$\begin{array}{@{}rcl@{}} \tau_{n}(\mu,\sigma) <0, && \text{if}\enspace \sigma > \lambda_{n}(\mu), \end{array} $$

(9)

for $n = 1,\ldots,\mathcal {N}$.

Remark 2.1.

The reason for introducing the surrogate eigenvalue problem (3) is that when the condition (8) is achieved, the right hand side of (3) vanishes and we can consider the left hand side in isolation as a linear problem to which we apply the SCRBE method, as described in the following sections. Two points have to be make clear about the parameter σ:

σ is meant to approximate a given eigenvalue λ _n(μ) of the original eigenproblem (1) by virtue of property (8),
the value for which σ=λ _n(μ) will be automatically determined by a direct search algorithm as presented in Section ‘Eigenvalue computation’.

Static condensation

We now move to the component level. We suppose that the system domain is naturally decomposable into I interconnected parametrized components. Each component i is associated with a subdomain Ω _i, where

$$\overline{\Omega} = \bigcup\limits_{i=1}^{I} \overline{\Omega}_{i}, \qquad \Omega_{i} \cap \Omega_{i'} = \emptyset, \text{for}\ i \neq i' \ . $$

We now introduce the notion of “port” that is commonly used in the literature related to CMS methods. A port corresponds to the interface shared by two components that are connected together. When looking at the global system, we will describe the ports as global, whereas when considering a single component, we will describe the ports as local. We say that components i and i ^′ are connected at global port p if $\overline \Omega _{i} \cap \overline \Omega _{i'}=\Gamma _{p}\neq \emptyset $, where 1≤p≤n ^Γ and n ^Γ is the total number of global ports in the system. We also say that ${\gamma _{i}^{j}}=\Gamma _{p}$ and $\gamma _{i'}^{j'}=\Gamma _{p}$ are local ports of components i and i ^′ respectively, where $1\leq j \leq n_{i}^{\gamma }$ is the total number of local ports in component i. Figure 1 shows an example of a three component system, with the corresponding global and local port definitions.

Figure 1
An example of system composed of three components, of indices 1, 2 and 3, corresponding to the subdomains Ω ₁,Ω ₂,Ω ₃. This system has two global ports of indices 1 and 2, corresponding to the interfaces $\Gamma _{1}=\overline \Omega _{1} \cap \overline \Omega _{2}$ and $\Gamma _{2}=\overline \Omega _{2} \cap \overline \Omega _{3}$. Component 1 has one local port ${\gamma _{1}^{1}}=\Gamma _{1}$, component 2 has two local ports ${\gamma _{2}^{1}}=\Gamma _{1}$ and ${\gamma _{2}^{2}}=\Gamma _{2}$, and component 3 has one local port ${\gamma _{3}^{1}}=\Gamma _{2}$.

We assume that the FE space $X^{\mathcal {N}}$ conforms to our components and ports, hence we can define the discrete spaces $X_{i}^{\mathcal {N}}$ and $Z_{p}^{\mathcal {N}}$ that are simply the restrictions of $X^{\mathcal {N}}$ to component i and global port p. For given i, let $X^{\mathcal {N}}_{i;0}$ denote the “component bubble space” — the restriction of $X^{\mathcal {N}}$ to Ω _i with homogeneous Dirichlet boundary conditions on each ${\gamma _{i}^{j}}, 1\leq j \leq n_{i}^{\gamma }$,

$$X^{\mathcal{N}}_{i ; 0} \equiv \left\{ v|_{\Omega_{i}} \colon v \in X^{\mathcal{N}}; \: v |_{{\gamma_{i}^{j}}} = 0, \, 1\leq j\leq n_{i}^{\gamma}\right\}. $$

We denote by $\mathcal {N}_{p}^{\Gamma }$ the dimension of the port space $Z_{p}^{\mathcal {N}}$ associated with global port p, and we say that the global port p has $\mathcal {N}_{p}^{\Gamma }$ degrees of freedom (dof). For each component i, we denote by k ^′ a local port dof number, and K _i the total numbers of dof on its local ports, such that 1≤k ^′≤K _i. We then introduce the map $\mathcal {P}_{i}(k')=(p,k)$ which associate a local port dof k ^′ in component i to its global port representation: global port p and dof k, $1\leq k \leq \mathcal {N}_{p}^{\Gamma }$.

To formulate our static condensation procedure we must first introduce the basis functions for the port space $Z_{p}^{\mathcal {N}}$ as $\{\zeta _{p,1},\cdots,\zeta _{p,\mathcal {N}_{p}^{\Gamma }}\}$. The particular choice for these functions is not important for now, but it becomes critical when dealing with port reduction – we refer to Section ‘Port reduction’. For a local port dof number k ^′ such that $\mathcal {P}_{i}(k')=(p,k)$, we then introduce the interface function $\psi ^{i}_{k'} \in X^{\mathcal {N}}_{i}$, which is the harmonic extension of the associated port space basis function into the interior of the component domain Ω _i, and satisfies

$$ \int_{\Omega_{i}} \nabla \psi^{i}_{k'} \cdot \nabla v = 0,\enspace \forall v \in X^{\mathcal{N}}_{i ; 0}, $$

(10)

$$ \psi^{i}_{k'} = \left\{ \begin{array}{ll} \zeta_{p,k} & \text{on}\,\, \Gamma_{p} \\ 0 & \text{on}\,\, {\gamma_{i}^{j}} \neq \Gamma_{p}, \ 1\leq j \leq n_{i}^{\gamma}. \end{array} \right. $$

(11)

We show in Figure 2 an example of port basis functions and interface functions.

Figure 2
Top row, an example of 4 port basis functions for a 2D square port. Bottom row, the corresponding interface functions in a beam component with the square port at one end.

If components i and j are connected, then for each matching local port dofs k _i and k _j such that $\mathcal {P}_{i}(k_{i})=\mathcal {P}_{j}(k_{j})=(p,k)$, we define the global interface function $\Psi _{p,k}\in X^{\mathcal {N}}$ as

$$ \Psi_{p,k}= \left\{ \begin{array}{ll} \psi^{i}_{k_{i}} & \text{on}\ \Omega_{i} \\ \psi^{j}_{k_{j}} & \text{on}\ \Omega_{j} \\ 0 & \text{elsewhere}. \end{array} \right. $$

(12)

We will now develop an expression for χ _n(μ) which just involves dof on the ports by virtue of elimination of the interior dof given that σ=λ _n(μ) – starting from (13) to finally arrive at (18). Let us suppose that we set σ=λ _n(μ) (for some n) so that the right-hand side of (3) vanishes. Then, for $\chi _{n}(\mu) \in X^{\mathcal {N}}$ we have

$$\mathcal{B}(\chi_{n}(\mu),v;\mu;\sigma) = 0, \quad \text{for all}\ v \in X^{\mathcal{N}}. $$

We then express $\chi _{n}(\mu) \in X^{\mathcal {N}}$ in terms of “interface” and “bubble” contributions,

$$ \chi_{n}(\mu) = \sum_{i=1}^{I} b_{i}(\mu,\sigma) + \sum_{p=1}^{n^{\Gamma}}\sum_{k=1}^{\mathcal{N}_{p}^{\Gamma}}U_{p,k}(\mu,\sigma)\Psi_{p,k}, $$

(13)

where the U _p,k(μ,σ) are interface function coefficients corresponding to the port p, and $b_{i}(\mu,\sigma) \in X_{i;0}^{\mathcal {N}}$. Here χ _n is independent of σ, but we shall see shortly that we will need b _i and U _k,p to be σ-dependent in general.

We then restrict to a single component i to obtain

$$ \mathcal{B}_{i}(\chi_{n}(\mu),v;\mu;\sigma) = 0, \quad \text{for all}\ v \in X^{\mathcal{N}}_{i;0}, $$

(14)

where $\mathcal {B}_{i}(w,v;\mu ;\sigma) \equiv a_{i}(w,v;\mu) - \sigma m_{i}(w,v;\mu)$, and where a _i and m _i indicate the restrictions of a and m to Ω _i, respectively. Substitution of (13) into (14) leads to

$$ \mathcal{B}_{i}(b_{i}(\mu,\sigma),v;\mu;\sigma) + \sum_{k=1}^{K_{i}}U_{\mathcal{P}_{i}(k)}(\mu,\sigma)\mathcal{B}_{i}(\psi_{i,k},v;\mu;\sigma) = 0, $$

(15)

for all $v \in X^{\mathcal {N}}_{i;0}$.

It can be shown from linearity of the above equation that we can reconstruct b _i(μ,σ) as

$$b_{i}(\mu,\sigma) = \sum_{k=1}^{K_{i}}U_{\mathcal{P}_{i}(k)}(\mu,\sigma) b_{i,k}(\mu,\sigma), $$

where $b_{i,k}(\mu,\sigma) \in X_{i;0}^{\mathcal {N}}$ satisfies

$$ \mathcal{B}_{i}(b_{i,k}(\mu,\sigma),v;\mu;\sigma) = - \mathcal{B}_{i}(\psi_{i,k},v;\mu;\sigma), \quad \forall v \in X_{i;0}^{\mathcal{N}}. $$

(16)

Let $(\lambda _{i,n}(\mu),\chi _{i,n}(\mu)) \in \mathbb {R} \times X_{i;0}^{\mathcal {N}}$ denote an eigenpair associated with the n local eigenproblem

$$ a_{i}(\chi_{i,n}(\mu),v;\mu) = \lambda_{i,n}(\mu) m_{i}(\chi_{i,n}(\mu),v;\mu), \quad \forall v \in X_{i;0}^{\mathcal{N}}, $$

(17)

then, since

$$\begin{array}{@{}rcl@{}} \inf_{v \in X_{i;0}^{\mathcal{N}}} \frac{\mathcal{B}_{i}(v,v;\mu;\sigma)}{\|v\|_{X,i}^{2}} &=& \inf_{v \in X_{i;0}^{\mathcal{N}}} \frac{a_{i}(v,v;\mu) - \sigma m_{i}(v,v;\mu)}{\|v\|_{X,i}^{2}}\\ &\geq& \inf_{v \in X_{i;0}^{\mathcal{N}}} \frac{a_{i}(v,v;\mu) - \sigma m_{i}(v,v;\mu)}{m_{i}(v,v;\mu)} \inf_{v \in X_{i;0}^{\mathcal{N}}} \frac{m_{i}(v,v;\mu)}{\|v\|_{X,i}^{2}}\\ &=& (\lambda_{i,1}(\mu) - \sigma) \inf_{v \in X_{i;0}^{\mathcal{N}}} \frac{m_{i}(v,v;\mu)}{\|v\|_{X,i}^{2}}, \end{array} $$

the bilinear form $\mathcal {B}_{i}(\cdot,\cdot ;\mu ;\sigma)$ is coercive on $X_{i;0}^{\mathcal {N}}$ if σ<λ _i,1(μ), where λ _i,1(μ) is the smallest eigenvalue of (17). Hence (16) has a unique solution under this condition. Note that we expect that λ _i,1(μ)>λ ₁(μ), and even λ _i,1(μ)>λ _n(μ) for n=2 or 3 or 4 — of course in practice the balance between λ _n and $\lambda _{i,n^{\prime }}$ will depend on the details of a particular problem.

Now for $1\leq k \leq \mathcal {N}_{p}^{\Gamma }$ and each p, let

$$\Phi_{p,k}(\mu,\sigma) = \Psi_{p,k} + \sum_{i,k' s.t. P_{i}(k')=(p,k)} b_{i,k'}(\mu,\sigma), $$

and let us define the “skeleton” space $X_{\mathcal {S}}(\mu,\sigma)$ as

$$X_{\mathcal{S}}(\mu,\sigma) \equiv \text{span}\{\Phi_{p,k}(\mu,\sigma):1\leq p \leq n^{\Gamma}, 1 \leq k \leq \mathcal{N}_{p}^{\Gamma}\}. $$

This space is of dimension $n_{\text {sc}}=\sum _{p=1}^{n^{\Gamma }} \mathcal {N}_{p}^{\Gamma }$.

Remark 2.2.

Note that the interface functions are intermediate quantities that are completed with bubble functions. Although the interface functions are the result of a simple harmonic lifting with the homogeneous Laplace operator, the subsequent bubble functions are computed based on the problem-dependent a and m bilinear forms, hence they capture the possible heterogeneities intrinsic to the problem. Hence the skeleton space $X_{\mathcal {S}}(\mu,\sigma)$ is suitable for approximation.

We restrict (13) to a single component i to see that for σ=λ _n(μ) we obtain

$$\chi_{n}(\mu)|_{\Omega_{i}} = \sum_{k=1}^{K_{i}} U_{\mathcal{P}_{i}(k)}(\mu,\sigma) \left(b_{i,k}(\mu,\sigma) + \psi_{i,k}\right). $$

This then implies

$$ \chi_{n}(\mu) = \sum_{p=1}^{n^{\Gamma}} \sum_{k=1}^{\mathcal{N}_{p}^{\Gamma}} \ U_{p,k}(\mu,\sigma) \: \Phi_{p,k}(\mu,\sigma) \in X_{\mathcal{S}}(\mu,\sigma). $$

(18)

Then, for σ=λ _n(μ) and $\mu \in \mathcal {D}$, we are able to solve for the coefficients U _p,k(μ,σ) from the static condensation eigenvalue problem on $X_{\mathcal {S}}(\mu,\sigma)$: find $\chi _{n}(\mu) \in X_{\mathcal {S}}(\mu,\sigma)$, such that

$$\begin{array}{@{}rcl@{}} \mathcal{B}(\chi_{n}(\mu),v;\mu;\sigma) &=& 0, \quad \forall v \in X_{\mathcal{S}}(\mu,\sigma),\quad \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} a(\chi_{n}(\mu),\chi_{n}(\mu);\mu) &=& 1. \end{array} $$

(20)

We now relax the condition σ=λ _n(μ) to obtain the following problem: For σ∈[0,σ _max] and $\mu \in \mathcal {D}$, find $(\overline {\tau }_{n}(\mu,\sigma),\overline {\chi }_{n}(\mu,\sigma)) \in (\mathbb {R}, X_{\mathcal {S}}(\mu,\sigma))$, such that

$$\begin{array}{@{}rcl@{}} \mathcal{B}(\overline{\chi}_{n}(\mu,\sigma),v;\mu;\sigma) &=& \overline{\tau}_{n}(\mu,\sigma)a(\overline{\chi}_{n}(\mu;\sigma),v;\mu), \quad \forall v \in X_{\mathcal{S}}(\mu,\sigma), \qquad \end{array} $$

(21)

$$\begin{array}{@{}rcl@{}} a(\overline{\chi}_{n}(\mu,\sigma),\overline{\chi}_{n}(\mu,\sigma);\mu) &=& 1. \end{array} $$

(22)

It is important to note that this new eigenproblem (21) (22) differs from (3) (4) in two ways: first, we consider a subspace $X_{\mathcal {S}}(\mu,\sigma)$ of $X^{\mathcal {N}}$, and as a consequence $\overline {\tau }_{n}(\mu,\sigma) \geq \tau _{n}(\mu,\sigma)$; second, the subspace $X_{\mathcal {S}}(\mu,\sigma)$, unlike $X^{\mathcal {N}}$, depends on σ, and furthermore only for σ=λ _n does the subspace $X_{\mathcal {S}}(\mu,\sigma)$ reproduce the eigenfunction χ _n(μ). We now show

Proposition 2.1.

Suppose σ<λ _i,1(μ) for each 1≤i≤I to ensure that the static condensation is well-posed.

(i)

$\overline {\tau }_{n}(\mu,\sigma) \geq \tau _{n}(\mu,\sigma)$, $n=1,\ldots,\text {dim}(X_{\mathcal {S}}(\mu,\sigma))$,
(ii)

τ _n(μ,σ)=0 if and only if σ=λ _n(μ),
(iii)

σ=λ _n(μ) if and only if there exists some n ^′ such that $\overline {\tau }_{n'}(\mu,\sigma) = 0$.

Proof.

(i)

The case n=1 follows from the Rayleigh quotients
$$ \tau_{1}(\mu,\sigma) = \inf_{w \in X^{\mathcal{N}}} \frac{\mathcal{B}(w,w;\mu;\sigma)}{a(w,w;\mu)}, $$

(23)

and
$$ \overline{\tau}_{1}(\mu,\sigma) = \inf_{w \in X_{\mathcal{S}}(\mu,\sigma)} \frac{\mathcal{B}(w,w;\mu;\sigma)}{a(w,w;\mu)}, $$

(24)

and fact that $X_{\mathcal {S}}(\mu,\sigma) \subset X^{\mathcal {N}}$.

For n>1, the Courant-Fischer-Weyl min-max principle [17] states that for an arbitrary n-dimensional subspace of $X^{\mathcal {N}}$, S _n, we have
$$ \eta_{n}(\mu,\sigma) \equiv \max_{w \in S_{n}} \frac{\mathcal{B}(w,w;\mu;\sigma)}{a(w,w;\mu)} \geq \tau_{n}(\mu,\sigma). $$

(25)

Let $S_{n} \equiv \text {span}\{ \overline {\chi }_{m}(\mu,\sigma), m=1,\ldots,n\} \subset X_{\mathcal {S}}(\mu,\sigma)$. Then $\eta _{n}(\mu,\sigma) = \overline {\tau }_{n}(\mu,\sigma)$, and the result follows.
(ii)

This equivalence is due to (8).
(iii)

(⇐) Suppose σ=λ _n(μ) for some n, then by construction $\chi _{n}(\mu,\sigma) \in X_{\mathcal {S}}(\mu,\sigma)$. Since the same operator 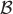appears in both (19) and (21), it follows that χ _n(μ,σ) is also eigenmode for (21), (22) with corresponding eigenvalue 0. That is, for some n ^′, $\overline {\tau }_{n'}(\mu,\sigma) = 0$ is an eigenvalue of (21), (22).

(⇒) Suppose $\overline {\tau }_{n'}(\mu,\sigma) = 0$ for some index n ^′. Then $\overline {\chi }_{n'}(\mu,\sigma)$ satisfies (19), (20), or equivalently, (3), (4) for τ _n(μ,σ)=0. From part (ii) of this Proposition, this implies that σ=λ _n(μ).

Remark 2.3.

Regarding our method, the main result is 2.1(iii), which informs on how to recover eigenvalues of the original problem (3), (4) from the shifted and condensed problem (21), (22): we look for the values of σ such that (21), (22) has a zero eigenvalue. Note that in 2.1(iii), the equivalence between $\overline {\tau }_{n'}(\mu,\sigma) = 0$ and σ=λ _n(μ) possibly happens for n ^′≠n. In practice though, we always have n ^′=n and there is a one-to-one correspondence between the original problem and the shifted and condensed system which make the eigenvalues much easier to track. We are not able to demonstrate that n ^′=n in all cases, but assuming that property, we can demonstrate some stronger properties (see 4) that we will use to derive error estimates.

To assemble an algebraic system for the static condensation eigenproblem, we insert (18) into (21), (22) to arrive at

$$\begin{array}{@{}rcl@{}} &&\sum_{p=1}^{n^{\Gamma}}\sum_{k=1}^{\mathcal{N}_{p}^{\Gamma}}U_{p,k}(\mu,\sigma) \mathcal{B}(\Phi_{p,k}(\mu,\sigma),v;\mu;\sigma) \\ &&= \overline{\tau}(\mu,\sigma)\sum_{p=1}^{n^{\Gamma}}\sum_{k=1}^{\mathcal{N}_{p}^{\Gamma}}U_{p,k}(\mu,\sigma) a(\Phi_{p,k}(\mu,\sigma),v;\mu;\sigma), \quad \forall v \in X_{\mathcal{S}}, \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} && \sum_{p=1}^{n^{\Gamma}}\sum_{k=1}^{\mathcal{N}_{p}^{\Gamma}}U_{p,k}(\mu,\sigma) a(\Phi_{p,k}(\mu,\sigma),\Phi_{p,k}(\mu,\sigma);\mu;\sigma)= 1. \end{array} $$

(27)

We now define our local stiffness and mass matrices $\mathbb {A}^{i}(\mu,\sigma), \mathbb {M}^{i}(\mu,\sigma) \in \mathbb {R}^{K_{i}\times K_{i}}$ for component i, which have entries

$$\begin{array}{@{}rcl@{}} \mathbb{A}^{i}_{k',k}(\mu,\sigma) &=& a_{i}(\psi_{i,k}+b_{i,k}(\mu,\sigma),\psi_{i,k'}+b_{i,k'}(\mu,\sigma);\mu), \\ \mathbb{M}^{i}_{k',k}(\mu,\sigma) &=& m_{i}(\psi_{i,k}+b_{i,k}(\mu,\sigma),\psi_{i,k'}+b_{i,k'}(\mu,\sigma);\mu), \end{array} $$

for 1≤k,k ^′≤K _i. We may then assemble the global system with matrices $\mathbb {B}(\mu,\sigma),\mathbb {A}(\mu,\sigma) \in \mathbb {R}^{n_{\textit {sc}}\times n_{\textit {sc}}}$, of dimension $n_{\textit {sc}}=\sum _{p=1}^{n^{\Gamma }}\mathcal {N}_{p}^{\Gamma }$: given a $\sigma \in \mathbb {R}$ and $\mu \in \mathcal {D}$, we consider the eigenproblem

$$\begin{array}{@{}rcl@{}} \mathbb{B}(\mu,\sigma)\mathbb{V}(\mu,\sigma) &=& \overline{\tau}(\mu,\sigma)\mathbb{A}(\mu,\sigma){\mathbb{V}}(\mu,\sigma), \end{array} $$

(28)

$$\begin{array}{@{}rcl@{}} \mathbb{V}(\mu,\sigma)^{T}\mathbb{A}(\mu,\sigma)\mathbb{V}(\mu,\sigma) &=& 1, \end{array} $$

(29)

where

$$ \mathbb{B}(\mu,\sigma) \equiv \mathbb{A}(\mu,\sigma)-\sigma\mathbb{M}(\mu,\sigma). $$

(30)

As explained above, in order to find the eigenvalues of the original problem (3), (4), we need to find the values of σ for which (28), (29) has a zero eigenvalue. When performing this search, for each new value of σ that is considered, we need to perform the assembly of the static condensation system (28), which involves many finite element computations at the component level in order to get the bubble functions (16), and is potentially costly. Note that we also need to reassemble (28) when the parameters μ of the problem change. In order to dramatically reduce the computational cost of this assembly, we will use reduced order modeling techniques as described in the next Sections ‘Reduced basis static condensation system’ and ‘Port reduction’.

Reduced basis static condensation system

Reduced basis bubble approximation

In the static condensation reduced basis element (SCRBE) method [10], we replace the FE bubble functions b _i,k(μ,σ) with reduced basis approximations. These RB approximations are significantly less expensive to evaluate (following an RB “offline” preprocessing step) than the original FE quantities, and hence the computational cost associated with the formation of the (now approximate) static condensation system is significantly reduced. We thus introduce the RB bubble function approximations

$$ \tilde{b}_{i,k}(\mu,\sigma) \approx b_{i,k}(\mu,\sigma) $$

(31)

for a parameter domain $(\mu,\sigma) \in \mathcal {D}\times [0,\sigma _{\max }]$, where

$$\sigma_{\max} = \epsilon_{\sigma}\min_{\mu \in \mathcal{D}} \min\limits_{1\leq i\leq I}\lambda_{i,1}(\mu). $$

(32)

Here ε _σ(<1) is a “safety factor” which ensures that we honor the condition σ<λ _i,1(μ) for all 1≤i≤I. Next, we let

$$\widetilde\Phi_{p,k}(\mu,\sigma) = \Psi_{p,k} + \sum_{i,k_{i} s.t. P_{i}(k_{i})=(p,k)} \tilde b_{i,k_{i}}(\mu,\sigma), $$

and define our RB static condensation space $\widetilde {X}_{\mathcal {S}}(\mu,\sigma) \subset X^{\mathcal {N}}$ as

$$\widetilde{X}_{\mathcal{S}}(\mu,\sigma) = \text{span}\{\widetilde{\Phi}_{p,k}(\mu,\sigma):1\leq p\leq n^{\Gamma}, 1 \leq k \leq \mathcal{N}_{p}^{\Gamma}\}. $$

(Note that $\widetilde {X}_{\mathcal {S}}(\mu,\sigma) \not \subset X_{\mathcal {S}}(\mu,\sigma)$).

Remark 3.1.

As opposed to CMS where the static condensation space is built from local component natural modes, the RB static condensation space $\widetilde {X}_{\mathcal {S}}(\mu,\sigma)$ is built from RB bubbles that can accommodate for any global mode shape thanks to their (μ,σ) parametrization. The only restriction is due to condition (32) which means that we only ensure to capture global modes for which the wavelength is typically greater than a component’s size.

We then define the RB eigenproblem: given $(\mu,\sigma) \in \mathcal {D}\times [0,\sigma _{\text {max}}]$, find the eigenpairs $(\widetilde {\overline {\tau }}_{n}(\mu,\sigma),\widetilde {\mathbb {V}}_{n}(\mu,\sigma))$ that satisfy

$$\begin{array}{@{}rcl@{}} \widetilde{\mathbb{B}}(\mu,\sigma)\widetilde{\mathbb{V}}(\mu,\sigma) &=& \widetilde{\overline{\tau}}(\mu,\sigma)\widetilde{\mathbb{A}}(\mu,\sigma)\widetilde{\mathbb{V}}(\mu,\sigma), \end{array} $$

(33)

$$\begin{array}{@{}rcl@{}} \widetilde{\mathbb{V}}(\mu,\sigma)^{T}\widetilde{\mathbb{A}}(\mu,\sigma)\widetilde{\mathbb{V}}(\mu,\sigma) &=& 1, \end{array} $$

(34)

where $\widetilde {\mathbb {B}}(\mu,\sigma),\widetilde {\mathbb {A}}(\mu,\sigma)$ are constructed component-by-component from

$$\begin{array}{@{}rcl@{}} \widetilde{\mathbb{A}}^{i}_{k',k}(\mu,\sigma) &=& a_{i}(\psi_{i,k}+\tilde{b}_{i,k}(\mu,\sigma),\psi_{i,k'}+\tilde{b}_{i,k'}(\mu,\sigma);\mu), \end{array} $$

(35)

$$\begin{array}{@{}rcl@{}} \widetilde{\mathbb{M}}^{i}_{k',k}(\mu,\sigma) &=& m_{i}(\psi_{i,k}+\tilde{b}_{i,k}(\mu,\sigma),\psi_{i,k'}+\tilde{b}_{i,k'}(\mu,\sigma);\mu), \end{array} $$

(36)

for 1≤k,k ^′≤K _i, and where

$$ \widetilde{\mathbb{B}}^{i}(\mu,\sigma) \equiv \widetilde{\mathbb{A}}^{i}(\mu,\sigma)-\sigma\widetilde{\mathbb{M}}^{i}(\mu,\sigma). $$

(37)

Reduced basis error estimator

We now consider error estimation for our RB approximations. In order to derive error estimates, we will use Hypothesis A.1 which is related to Remark 2.3, and reads

$$\sigma = \lambda_{n}(\mu) \Leftrightarrow \overline{\tau}_{n}(\mu,\sigma) = 0.$$

Note that this hypothesis is solely used for error estimation, the computational method itself does not rely on this assumption.

First, since $\widetilde {X}_{\mathcal {S}}(\mu,\sigma) \subset X^{\mathcal {N}}$, by the same argument as part (i) of Proposition 2.1, we have

Corollary 3.1.

$$ \widetilde{\overline{\tau}}_{n}(\mu,\sigma) \geq \tau_{n}(\mu,\sigma), \quad n=1,2,\ldots,n_{\text{sc}}. $$

(38)

□

We define the residual $r_{i,k}(\cdot ;\mu,\sigma):X_{i;0}^{\mathcal {N}} \to \mathbb {R}$ for 1≤k≤K _i, and 1≤i≤I as

$$ r_{i,k}(v;\mu,\sigma) = - \mathcal{B}_{i}(\psi_{i,k}+\tilde b_{i,k}(\mu,\sigma),v;\mu,\sigma), \quad \forall v \in X_{i;0}^{\mathcal{N}}, $$

and the error bound [4]

$$\|b_{i,k}(\mu,\sigma) - \tilde b_{i,k}(\mu,\sigma)\|_{X,i} \leq \widetilde\Delta_{i,k}(\mu,\sigma) = \frac{\mathcal{R}_{i,k}(\mu,\sigma)}{\alpha^{\text{LB}}_{i}(\mu,\sigma)}, $$

where

$$\mathcal{R}_{i,k}(\mu,\sigma) = \sup_{v \in X^{\mathcal{N}}_{i;0}} \frac{r_{i,k}(v;\mu,\sigma)}{\|v\|_{X,i}}$$

is the dual norm of the residual, and $\alpha ^{\text {LB}}_{i}(\mu,\sigma)$ is a lower bound for the coercivity constant

$$\alpha_{i}(\mu,\sigma) = \inf_{w \in X_{i;0}^{\mathcal{N}}}\frac{\mathcal{B}_{i}(w,w;\mu,\sigma)}{\|w\|^{2}_{X,i}}, $$

that can be derived by hand for simple cases, or computed using a successive constraint linear optimization method [18].

We now assume that Hypothesis A.1 holds. Suppose we have found σ _n, the n ^th “shift” such that $\widetilde {\mathbb {B}}(\mu,\sigma _{n})$ has a zero eigenvalue, i.e. we have $\widetilde {\overline {\tau }}_{n}(\mu,\sigma _{n})=0$. Then our RB-based approximation to the n ^th eigenvalue is $\tilde {\lambda }_{n}(\mu) = \sigma _{n}$. We will now develop a first order error estimator for $\overline {\tau }_{n}(\mu,\sigma _{n})$. We have

$$\mathbb{B}(\mu,\sigma_{n})\mathbb{V}(\mu,\sigma_{n}) = \overline{\tau}_{n}(\mu,\sigma_{n})\mathbb{A}(\mu,\sigma_{n})\mathbb{V}(\mu,\sigma_{n}), $$

and hence with $\mathbb {B}(\mu,\sigma _{n}) \equiv \widetilde {\mathbb {B}}(\mu,\sigma _{n})+\delta \mathbb {B}(\mu,\sigma _{n})$, $\mathbb {A}(\mu,\sigma _{n}) \equiv \widetilde {\mathbb {A}}(\mu,\sigma _{n})+\delta \mathbb {A}(\mu,\sigma _{n})$, ${\mathbb {V}}(\mu,\sigma _{n}) \equiv \widetilde {\mathbb {V}}(\mu,\sigma _{n})+\delta \mathbb {V}(\mu,\sigma _{n})$, we obtain

$$\begin{array}{*{20}l} &(\widetilde{\mathbb{B}}(\mu,\sigma_{n})+\delta\mathbb{B}(\mu,\sigma_{n}))(\widetilde{\mathbb{V}}(\mu,\sigma_{n}) +\delta{\mathbb{V}}(\mu,\sigma_{n})) =\\ &\overline{\tau}_{n}(\mu,\sigma_{n})(\widetilde{\mathbb{A}}(\mu,\sigma_{n})+\delta{\mathbb{A}}(\mu,\sigma_{n})) (\widetilde{{\mathbb{V}}}(\mu,\sigma_{n})+\delta{\mathbb{V}}(\mu,\sigma_{n})). \end{array} $$

(39)

Expansion of the above expression yields

$$\begin{array}{*{20}l} &\widetilde{\mathbb{B}}(\mu,\sigma_{n})\delta{\mathbb{V}}(\mu,\sigma_{n}) + \delta{\mathbb{B}}(\mu,\sigma_{n})\widetilde{{\mathbb{V}}}(\mu,\sigma_{n}) + \delta{\mathbb{B}}(\mu,\sigma_{n})\delta\mathbb{V}(\mu,\sigma_{n}) = \\ &\overline{\tau}_{n}(\mu,\sigma_{n})(\widetilde{\mathbb{A}}(\mu,\sigma_{n})\widetilde{{\mathbb{V}}}(\mu,\sigma_{n}) + \widetilde{\mathbb{A}}(\mu,\sigma_{n})\delta\mathbb{V}(\mu,\sigma_{n}) +\\& \delta{\mathbb{A}}(\mu,\sigma_{n})\widetilde{{\mathbb{V}}}(\mu,\sigma_{n}) + \delta{\mathbb{A}}(\mu,\sigma_{n})\delta{\mathbb{V}}(\mu,\sigma_{n})), \end{array} $$

(40)

where the identity $\widetilde {\mathbb {B}}(\mu,\sigma _{n})\widetilde {\mathbb {V}}(\mu,\sigma _{n}) = 0$ has been employed. We then multiply through by $\widetilde {\mathbb {V}}(\mu,\sigma _{n})^{T}$ and note that

$$\begin{array}{*{20}l} &\widetilde{{\mathbb{V}}}(\mu,\sigma_{n})^{T}\widetilde{\mathbb{B}}(\mu,\sigma_{n})\delta\mathbb{V}(\mu,\sigma_{n}) =\delta\mathbb{V}(\mu,\sigma_{n})^{T}\widetilde{\mathbb{B}}(\mu,\sigma_{n})\widetilde{\mathbb{V}}(\mu,\sigma_{n})= 0,\\ &\widetilde{{\mathbb{V}}}(\mu,\sigma_{n})^{T}\widetilde{\mathbb{A}}(\mu,\sigma_{n})\widetilde{{\mathbb{V}}}(\mu,\sigma_{n})=1 \end{array} $$

and neglect higher order terms to obtain

$$ \overline{\tau}_{n}(\mu,\sigma_{n}) \approx \widetilde{\mathbb{V}}(\mu,\sigma_{n})^{T}\delta\mathbb{B}(\mu,\sigma_{n})\widetilde{\mathbb{V}}(\mu,\sigma_{n}). $$

(41)

We then have the following bound

$$\begin{array}{*{20}l} |\widetilde{\mathbb{V}}(\mu&,\sigma_{n})^{T}\delta\mathbb{B}(\mu,\sigma_{n})\widetilde{\mathbb{V}}(\mu,\sigma_{n})| \\ &\leq \sum_{i=1}^{I} \sum_{k=1}^{K_{i}} \sum_{j=1}^{I} \sum_{l=1}^{K_{j}}|\widetilde{\mathbb{V}}_{\mathcal{P}_{i}(k)}(\mu,\sigma_{n})|\widetilde\Delta_{i,k}(\mu,\sigma_{n})\widetilde\Delta_{j,l}(\mu,\sigma_{n})|\widetilde{\mathbb{V}}_{\mathcal{P}_{j}(l)}(\mu,\sigma_{n})| \\ &\equiv \widetilde\Delta(\mu,\sigma_{n}). \end{array} $$

(42)

From Proposition 2.1 part (iii), we can only infer eigenvalues of (1),(2) when $\overline {\tau }_{n}(\mu,\sigma) = 0$, hence (42) does not give us a direct bound on the error of $\tilde {\lambda }_{n}(\mu)$. However, with the assumption that $\widetilde \Delta (\mu,\sigma _{n}) \to 0$ in the limit as N→∞, we see that $\overline {\tau }_{n}(\mu,\sigma _{n}) \to 0$ and hence asymptotically we have that $\tilde {\lambda }_{n}(\mu)$ converges to λ _n(μ). Moreover, we can develop an asymptotic error estimator. From Proposition A.1, we have

$$\begin{array}{*{20}l} \overline{\tau}_{n}(\mu,\tilde\lambda_{n}(\mu))&\approx \overline{\tau}_{n}(\mu,\lambda_{n}(\mu)) + (\tilde\lambda_{n}(\mu)-\lambda_{n}(\mu))\frac{\partial\overline{\tau}_{n}(\mu,\lambda_{n}(\mu))}{\partial\sigma} \\ &= \frac{\lambda_{n}(\mu)-\tilde\lambda_{n}(\mu)}{\lambda_{n}(\mu)}. \end{array} $$

(43)

Combining (42) and (43) gives the following asymptotic (relative) error estimator

$$ \frac{|\lambda_{n}(\mu)-\tilde\lambda_{n}(\mu)|}{\lambda_{n}(\mu)} \lesssim \widetilde\Delta(\mu,\sigma_{n}). $$

(44)

Port reduction

Empirical mode construction

In practice, for the basis functions of the port space $Z_{p}^{\mathcal {N}}$, we use a simple Laplacian eigenmode decomposition, corresponding to the eigenfunctions ζ _p,k of the following eigenproblem

$$\begin{array}{*{20}l} \int_{\Gamma_{p}} \nabla \zeta_{p,k} \cdot \nabla v = \Lambda_{p,k} \int_{\Gamma_{p}} \zeta_{p,k} v,\quad\forall v\in Z_{p}^{\mathcal{N}},\quad 1\leq k \leq {\mathcal{N}}_{p}^{\Gamma}. \end{array} $$

(45)

We can truncate the Laplacian eigenmode expansion in order to reduce ${\mathcal {N}}_{p}^{\Gamma }$ – often without any significant loss in accuracy of the method. However, we can obtain better results by tailoring the port basis functions to a specific class of problems. A strategy for the construction of such empirical port modes is presented in [16]. We briefly describe this strategy here and refer the reader to [16] for further detail.

A key observation is that, in a system of components, the solution on any given interior global port is “only” influenced by the parameter dependence of the two components that share this port and the solution on the non-shared ports of these two components. We shall exploit this observation to explore the solution manifold associated with a given port through a pairwise training algorithm.

To construct the empirical modes we first identify groups of local ports on the components which may interconnect; the port spaces for all ports in each such group must be identical. For each pair of local ports within each group (connected to form a global port Γ _p), we execute Algorithm (1): we sample this I=2 component system many (N _samples) times for random (typically uniformly or log-uniformly distributed) parameters over the parameter domain and for random boundary conditions on non-shared ports. For each sample we extract the solution on the shared port Γ _p; we then subtract its average and add the resulting zero-mean function to a snapshot set S _pair. Note that by construction all functions in S _pair are thus orthogonal to the constant function.

Upon completion of Algorithm 1 for all possible component connectivity within a library, we form a larger snapshot set S _group which is the union of all the snapshot sets S _pair generated for each pair. We then perform a data compression step: we invoke proper orthogonal decomposition (POD) [19] (with respect to the L ²(Γ _p) inner product). The output from the POD procedure is a set of mutually L ²(Γ _p)-orthonormal empirical modes that have the additional property that they are orthogonal to the constant mode.

Note that each POD compression step is done on a possibly large dataset of vectors, but for vectors of small size equal to the number of dofs of a given 2D port (for example the square port in Figure 3). Hence the POD procedure described here is computationally cheap, unlike POD for datasets of full 3D solution fields.

Figure 3
The component library: a beam (left) and a connector (right). Components can connect at square ports shown in red. All ports have the same shape and same discretization: a square of side 1 with square mesh cells of side 0.2. The size of the archetype beam is 1×1×5 with cubic mesh cells with side edges of length 0.2. The connector is a combination of several cubes with side edges of length 1, such that its length is 3 along each of the three principal axis. The connector mesh is refined at the joints between the cubes where we expect higher stresses.

Port-reduced system

In practice we use SCRBE – RB approximations for the bubble functions – but as we will see in the result section, the error introduced by RB approximation is very small and negligible compared to the error due to port reduction. As a consequence, we describe the port reduction procedure starting from the “truth” static condensation system (28), but we will in practice apply the port reduction to the SCRBE system (33). We recall that on port p the full port space is given as

$$\begin{array}{*{20}l} Z_{p}^{\mathcal{N}} = \left\{\zeta_{p,1},\cdots,\zeta_{p,\mathcal{N}_{p}^{\Gamma}}\right\}. \end{array} $$

(46)

For each port, we shall choose a desired port space dimension n _A,p such that $1\leq n_{\mathrm {A},p} \leq {\mathcal {N}}_{p}^{\Gamma }$. We shall then consider the basis functions ζ _k, 1≤k≤n _A,p, as the active port modes (hence subscript _A); we consider the $n_{\mathrm {I},p} = {\mathcal {N}}_{p}^{\Gamma } - n_{\mathrm {A},p}$ remaining basis functions ζ _k, $n_{\mathrm {A},p}+1 \leq k \leq {\mathcal {N}}_{p}^{\Gamma }$, as inactive (hence subscript _I). Note that $\text {span}\{\zeta _{p,1},\dotsc,\zeta _{p,n_{\mathrm {A},p}}\} \subseteq Z_{p}^{\mathcal {N}}$. We then introduce

$$\begin{array}{*{20}l} n_{\mathrm{A}} \equiv \sum_{p = 1}^{n^{\Gamma}} n_{{ \mathrm{A}},p}^{\Gamma},\qquad n_{\mathrm{I}} \equiv \sum_{p = 1}^{n^{\Gamma}} n_{{\mathrm{I}},p}^{\Gamma}, \end{array} $$

(47)

as the number of total active and inactive port modes, respectively; and n _SC=n _A+n _I is the total number of port modes in the non-reduced system.

Next, we assume a particular ordering of the degrees of freedom in (28): we first order the degrees of freedom corresponding to the n _A active system port modes and then by the degrees of freedom corresponding to the n _I inactive system port modes. We may then interpret (28) as

$$ \left[ \begin{array}{cc} \mathbb{B}_{\text{AA}}(\mu,\sigma) & \mathbb{B}_{\text{AI}}(\mu,\sigma) \\ \mathbb{B}_{\text{IA}}(\mu,\sigma) & \mathbb{B}_{\text{II}}(\mu,\sigma) \end{array} \right] \mathbb{V}(\mu,\sigma) = \overline{\tau}(\mu,\sigma) \left[\begin{array}{cc} \mathbb{A}_{\text{AA}}(\mu,\sigma) & \mathbb{A}_{\text{AI}}(\mu,\sigma) \\ \mathbb{A}_{\text{IA}}(\mu,\sigma) & \mathbb{A}_{\text{II}}(\mu,\sigma) \end{array}\right] \mathbb{V}(\mu,\sigma), $$

(48)

where the four blocks in the matrices correspond to the various couplings between active and inactive modes; note that $\mathbb {B}_{\text {AA}}(\mu)\in \mathbb {R}^{n_{\mathrm {A}} \times n_{\mathrm {A}}}$ and that $\mathbb {B}_{\text {II}}(\mu)\in \mathbb {R}^{n_{\mathrm {I}}\times n_{\mathrm {I}}}$. Our port-reduced approximation $\widehat {\overline {\tau }}(\mu,\sigma)$ shall be given as the solution to the n _A×n _A system

$$\begin{array}{*{20}l} \mathbb{B}_{\text{AA}}(\mu,\sigma)\mathbb{V}_{\mathrm{A}}(\mu,\sigma) &= \widehat{\overline{\tau}}(\mu,\sigma)\mathbb{A}_{\text{AA}}(\mu,\sigma)\mathbb{V}_{\mathrm{A}}(\mu,\sigma),\\ \mathbb{V}_{\mathrm{A}}(\mu,\sigma)^{T}\mathbb{A}_{\text{AA}}(\mu,\sigma)\mathbb{V}_{\mathrm{A}}(\mu,\sigma) &= 1 \end{array} $$

(49)

in which we may discard the (presumably large) $\mathbb {B}_{\text {II}}(\mu,\sigma)$ and $\mathbb {A}_{\text {II}}(\mu,\sigma)$ blocks; however the $\mathbb {B}_{\text {IA}}(\mu,\sigma)$-block is required later for residual evaluation in the context of a posteriori error estimation.

Port reduction error estimator

We put a $\enspace \widehat \cdot \enspace $ on top of all the port reduced quantities. In this section only we will use Hypothesis A.1 in order to derive error estimates, but note that the port reduction procedure does not require this assumption. Suppose we have found σ _n such that $\widehat {\overline {\tau }}_{n}(\mu,\sigma _{n})=0$ with eigenvector of size n _SC in the non-reduced space

$$\widehat{\mathbb{V}}_{n}(\mu,\sigma_{n})= \left[\begin{array}{c} \mathbb{V}_{\mathrm{A},n}(\mu,\sigma_{n}) \\ 0 \end{array}\right]. $$

We can expand $\widehat {\mathbb {V}}_{n}(\mu,\sigma _{n})$ in terms of the eigenvectors $\mathbb {V}_{m}(\mu,\sigma _{n})$ of the non reduced space

$$\widehat{\mathbb{V}}_{n}(\mu,\sigma_{n}) = \sum_{m=1}^{n_{\text{SC}}} \alpha_{m}(\mu,\sigma_{n}) \mathbb{V}_{m}(\mu,\sigma_{n}). $$

Since $\widehat {\overline {\tau }}_{n}(\mu,\sigma _{n})=0$, we can reasonably assume that $|\overline {\tau }_{n}(\mu,\sigma _{n})|=\min \limits _{1\leq m \leq n_{\text {SC}}}|\overline {\tau }_{m}(\mu,\sigma _{n})|$. We now look at the following residual

$$\begin{array}{*{20}l} \mathbb{B}(\mu,\sigma_{n}) \widehat{\mathbb{V}}_{n}(\mu,\sigma_{n}) &= \sum_{m=1}^{n_{\text{SC}}} \alpha_{m}(\mu,\sigma_{n}) \mathbb{B}(\mu,\sigma_{n}) \mathbb{V}_{m}(\mu,\sigma_{n})\\ &= \sum_{m=1}^{n_{\text{SC}}} \alpha_{m}(\mu,\sigma_{n}) \overline{\tau}_{m}(\mu,\sigma_{n}) \mathbb{A}(\mu,\sigma_{n}) \mathbb{V}_{m}(\mu,\sigma_{n}), \end{array} $$

so using the $\mathbb {A}(\mu,\sigma _{n})$ orthogonality of the $\mathbb {V}_{m}(\mu,\sigma _{n})$ we obtain

$$\begin{array}{*{20}l} \|\mathbb{B}(\mu,\sigma_{n}) &\widehat{\mathbb{V}}_{n}(\mu,\sigma_{n})\|^{2}_{\mathbb{A}(\mu,\sigma_{n})^{-1}} \\ & = \sum_{m=1}^{n_{\text{SC}}} |\overline{\tau}_{m}(\mu,\sigma_{n})|^{2} \|\alpha_{m}(\mu,\sigma_{n}) \mathbb{A}(\mu,\sigma_{n}) \mathbb{V}_{m}(\mu,\sigma_{n}) \|^{2}_{\mathbb{A}(\mu,\sigma_{n})^{-1}} \\ & \geq |\overline{\tau}_{n}(\mu,\sigma_{n})|^{2} \sum_{m=1}^{n_{\text{SC}}} \|\alpha_{m}(\mu,\sigma_{n}) \mathbb{A}(\mu,\sigma_{n}) \mathbb{V}_{m}(\mu,\sigma_{n}) \|^{2}_{\mathbb{A}(\mu,\sigma_{n})^{-1}} \\ & = |\overline{\tau}_{n}(\mu,\sigma_{n})|^{2} \| \sum_{m=1}^{n_{\text{SC}}} \alpha_{m}(\mu,\sigma_{n}) \mathbb{A}(\mu,\sigma_{n}) \mathbb{V}_{m}(\mu,\sigma_{n}) \|^{2}_{\mathbb{A}(\mu,\sigma_{n})^{-1}} \\ & = |\overline{\tau}_{n}(\mu,\sigma_{n})|^{2}, \end{array} $$

where we use the Euclidean norm derived from the $\mathbb {A}(\mu,\sigma _{n})^{-1}$ scalar product. We thus obtain the following error bound

$$\begin{array}{*{20}l} \widehat{\Delta}(\mu,\sigma_{n})\equiv\|\mathbb{B}(\mu,\sigma_{n}) \widehat{\mathbb{V}}_{n}(\mu,\sigma_{n})\|_{\mathbb{A}(\mu,\sigma_{n})^{-1}} \geq |\overline{\tau}_{n}(\mu,\sigma_{n})|. \end{array} $$

Finally, we recover an error estimator for the eigenvalue λ _n(μ) of the original eigenproblem. Assuming $\widehat \lambda _{n}(\mu)$ is close to λ _n(μ), we can then use Proposition A.1 as in (43), and we get the relative error estimator

$$\frac{|\lambda_{n}(\mu)-\widehat\lambda_{n}(\mu)|}{\lambda_{n}(\mu)} \lesssim \widehat\Delta(\mu,\sigma_{n}). $$

It is important to note that $\widehat \Delta (\mu,\sigma _{n})$ will only decrease linearly in the residual, whereas the actual eigenvalue error is expected to decrease quadratically in the residual. This is due to the fact that port reduction can be viewed as a Galerkin approximation over a subspace of the skeleton space $X_{\mathcal {S}}(\mu,\sigma)$, and in that framework several a priori and a posteriori error results demonstrate the quadratic convergence of the eigenvalue [20]. As a consequence the effectivity of the error estimator $\widehat \Delta (\mu,\sigma _{n})$ is expected to degrade as n _A,p gets larger.

Note that

$$\mathbb{B}(\mu,\sigma_{n}) \widehat{\mathbb{V}}_{n}(\mu,\sigma_{n})=\left[ \begin{array}{c} 0 \\ \mathbb{B}_{\text{IA}}(\mu,\sigma_{n})\mathbb{V}_{\mathrm{A},n}(\mu,\sigma_{n}) \end{array}\right], $$

and so the computation of the residual requires the additional assembly of $\mathbb {B}_{\text {IA}}(\mu,\sigma _{n})$, which does not generate an important extra computation since in practice we will consider n _A≪n _I. On the contrary, the computation of the norm $\|\cdot \|_{\mathbb {A}(\mu,\sigma _{n})^{-1}}$ requires the assembly and inversion of $\mathbb {A}(\mu,\sigma _{n})$, the full Schur complement stiffness matrix, which would potentially eliminate any speed-up obtained by the port reduction. This computational issue is resolved by using an upper bound for $\|\cdot \|_{\mathbb {A}(\mu,\sigma _{n})^{-1}}$ which is based on a non-conforming version $\mathbb {A}'(\mu,\sigma _{n})$ of the stiffness operator and a parameter independent preconditioner: the former permits online computation of small matrix inverses locally on each component, and the latter allows us to precompute non-reduced matrices and their Cholesky decompositions in an offline stage. The entire procedure is described in detail in [16].

Computational aspects

In this section, we summarize the main steps of the method from a computational point of view. There are two clearly separated stages. The “Offline” stage involves heavy pre-computations and is performed only once. The “Online” stage corresponds to the actual solution of the eigenproblem and can be performed many times for various parameters μ and different eigenvalue targets. The “Online” computations are very fast thanks to our approach and allow to solve eigenproblems in a many query context such as model optimization or design.

Offline computations

In the Offline stage, we already have some knowledge about the class of eigenproblems we will have to solve. We know the bilinear forms a and m corresponding to the stiffness and mass operators. We have a predefined library of archetype components that will be allowed to be connected together at compatible ports to form bigger systems that will be considered in the Online stage. See Figure 3 for an example of library, and Figure 6 for an example of system obtained from component assembly. Note that each archetype component in the library is allowed to have some parametric variability.

For each port type corresponding to a possible connection between archetype components, we perform the following computations:

Compute a set of port modes, possibly empirical modes as described in Section ‘Empirical mode construction’.

For each archetype component, we perform the following computations:

Compute the harmonic extension of the port modes inside the archetype component reference domain to get the interface functions.
For each interface function, compute a reduced basis space for the bubble Eq. 16. Each RB space is tuned for the stiffness and mass operators, as well as the component parametric variability and the shift σ variability.
Precompute some component quantities used in (35), (36), that will be ready in the Online stage for system assembly.

Online stage

System assembly. In the Online stage, we form a component assembly by instantiating I components from our library of archetype components, and connecting them together. Several instantiated components can correspond to the same archetype component, but with possibly different parameter values. Each instantiated component i has a set of parameter values μ _i, and the whole system has a set of parameters μ=∪_i=1..I μ _i. We also define a value of σ for the whole system.

For each instantiated component i, we perform the following computations:

Compute the RB approximations of the bubble functions for parameter values (μ _i,σ).
Compute the component stiffness and mass matrices (35), (36).

At the system level, we perform the following computations:

Assemble the system (33) for parameter values (μ,σ), using the component matrices (35), (36) previously computed for each instantiated component.

Eigenvalue computation. At this point, we now need to find the values of σ for which the system (33) has a zero eigenvalue. We proceed by fixing an eigenvalue number n and we then follow Algorithm 2 with tolerance δ≪1.

Applying this algorithm for n=1,2,3,… we can recover the first eigenvalues of the component assembly. In practice Brent’s method [21] applied to the search of σ such that $\widetilde {\overline {\tau }}_{n}(\mu,\sigma)=0$ converges in about 10 iterations, and there is only a single root for the function $\sigma \mapsto \widetilde {\overline {\tau }}_{n}(\mu,\sigma)$.

Once an approximation $\widetilde {\lambda _{n}}(\mu)=\sigma $ of the eigenvalue has been found, we obtain an associated eigenvector following (33). Note that we use a standard eigensolver from the SLEPc library [22] as a black box, hence we have no control on the eigenvector computation, especially when the eigenvalue multiplicity is two or more.

Remark 5.1.

The parametric dependence comes into play in the Online stage when the RB bubble functions are computed, as they depend on (μ,σ). As a consequence, the resulting shifted system depends on (μ,σ), and also its eigenvalues $\widetilde {\overline {\tau }}_{n}(\mu,\sigma)$. The vector of parameters μ is chosen by the user for the whole system (material properties of the different components, geometry), while σ is automatically updated at each step of Algorithm 2: as a result, the RB bubble functions have to be recomputed at each step of Algorithm 2. In the end though, we obtain an approximation $\widetilde {\lambda _{n}}(\mu)$ that depends only on μ, the “natural” parameters of the original system. The user is then free to modify the system by choosing a different vector of parameters μ ^′, and restart Algorithm 2.

Results and discussion

Linear elasticity

We consider linear elasticity in a non-dimensional form: we nondimensionalize space with respect to a length d ₀ which will correspond to the beam width in the following, we nondimensionalize the Young’s modulus E with respect to a reference value E ₀, and we nondimensionalize time with respect to $\sqrt {\frac {\rho d_{0}}{E_{0}}}$, where ρ is the mass density. The non dimensional linear elasticity free vibration equation then reads

$$ -\mathcal A U = \frac{\partial^{2} U}{\partial t^{2}}, $$

(50)

where

is a linear second order differential operator in space and U(x,t) is the displacement vector. Assuming that the free vibration solution is of the form U(x,t)=u(x)c o s(ω t), the problem is equivalent to solving the eigenproblem

$$ \mathcal A u = \omega^{2} u. $$

(51)

In variational form, the operator

corresponds to the bilinear form [4]

$$ a(w,v;\mu)\equiv\int_{\Omega(\mu)} C_{ijkl}(\mu)\epsilon_{ij}(w)\epsilon_{kl}(v) $$

(52)

where we assume summation on repeated indices; a(·,·;μ) is defined on the space of admissible displacements V={v=(v ₁,v ₂,v ₃)|v _i∈H ¹(Ω(μ));v _i=0onΓ ₀(μ)⊂∂ Ω(μ)}, and $\epsilon _{\textit {ij}}(v)=\frac {1}{2}(\partial _{i} v_{j} + \partial _{j} v_{i})$. We will consider piecewise isotropic materials, in which case the coefficients C _ijkl(μ) are functions of only two parameters at a given point in space: Poisson’s ratio ν and Young’s modulus E. In the following we always fix ν=0.3, and allow E to vary, hence E is part of the vector of parameters μ. More precisely, the parametric dependence reads

$$C_{ijkl}(\mu)=\frac{E \nu}{(1 + \nu) (1 - 2\nu)}\delta_{ij}\delta_{kl}+\frac{E }{ 2(1 + \nu)}(\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk}). $$

We also define the mass bilinear form

$$ m(w,v;\mu)\equiv\int_{\Omega(\mu)} w_{i} v_{i}. $$

(53)

Note that there is also a μ dependency coming from the possible geometrical variations, hence the notation Ω(μ). If we define a mapping function ϕ _μ such that Ω(μ)=ϕ _μ(Ω _ref), for a reference domain Ω _ref, then the mass bilinear form could also read:

$$ m(w,v;\mu)\equiv\int_{\Omega_{\text{ref}}} (w_{i} \circ \phi_{\mu})\cdot(v_{i} \circ \phi_{\mu}) |Jac(\phi_{\mu})|, $$

(54)

and a similar expression could be obtained for the stiffness bilinear form a(·,·;μ).

The eigenproblem in variational form finally reads: find $\lambda (\mu) \in \mathbb {R}_{> 0}$ and u(μ)∈V such that

$$\begin{array}{@{}rcl@{}} a(u(\mu),v;\mu) &=& \lambda(\mu)m(u(\mu),v;\mu), \quad \forall v \in V, \end{array} $$

(55)

$$\begin{array}{@{}rcl@{}} m(u(\mu),u(\mu);\mu) &=& 1. \end{array} $$

(56)

Note that λ(μ)=ω ²(μ) – the eigenvalue is the frequency squared.

Simple component library

We consider a linear elasticity library of two components shown in Figure 3: a beam and a connector. The FE hexahedral meshes are shown in Figure 3, and in all the following we use first order approximation with trilinear elements. The components can connect at square ports of dimension 1×1 with $\mathcal {N}_{p}^{\Gamma }=3\times 36=108$ degrees of freedom. The beam has two parameters: the Young’s modulus E∈[0.5,2] and the length scaling s∈[0.5,2], where the beam is of length 5s. The connector has one parameter, the Young’s modulus E∈[0.5,2]. Finally, for the shift parameter σ, we consider the range [0,0.01], based on the fact that the local minimum eigenvalues of the two components are larger than 0.01 for the previous E and s parameter ranges. For each component, we build RB bubble spaces of size N=10 using a Greedy algorithm [23], for the parameter ranges previously defined. See [4] for a detailed example of reduced basis applied to linear elasticity. We also perform a pairwise training for the component pair beam-connector to build empirical port modes as described in Section ‘Empirical mode construction’; and we build a parameter independent preconditioner (necessary for the computation of $\widehat \Delta $) using parameter values E=0.5 and s=0.5.

Simple beam

We first present a simple example where we compare with beam theory to demonstrate that the FE resolution is adequate and that we capture the different modes. We connect eight beam components together, corresponding to a system with a vector of parameters μ of dimension 16. By using the same values of s=1 and E=1 for all beam components – or equivalently $\mu =\mathbb {1}\in \mathbb {R}^{16}$ – we obtain a system corresponding to a uniform beam of square section, with thickness d=1 and length L=40, and Young’s modulus E=1. As boundary conditions, we clamp this beam on both ends.

Table 1 presents the first eight eigenvalues obtained by different methods: Euler Bernoulli model [24], Timoshenko model [24], global FEM and SCRBE with and without port reduction (in which the beam is constructed as the concatenation of eight beam components). The eigenvalues (which we recall are the frequencies squared) are quite small as the beam is of large aspect ratio. The SCRBE results are obtained by connecting eight beam components together with length parameter s=1, using RB spaces of size N=10; no port reduction corresponds to $n_{\text {A,p}}=\mathcal {N}_{p}^{\Gamma }=108$, and for port reduction we use n _A,p=20 active port modes. The global FEM results are obtained using a global mesh corresponding to eight beam component meshes stitched together, hence SCRBE and FEM are based on the same mesh and FE resolution.

Table 1

Eigenvalues for a clamped-clamped uniform beam of square section, with thickness d =1 and length L =40

	λ ₁	λ ₂	λ ₃	λ ₄
Euler Bernoulli	1.6294e-05	1.2381e-04	4.7583e-04	1.3003e-03
Timoshenko	1.6204e-05	1.2224e-04	4.6524e-04	1.2560e-03
Global FEM	1.6612e-05	1.2489e-04	4.7327e-04	1.2708e-03
SCRBE n _A,p=108	1.6612e-05	1.2489e-04	4.7327e-04	1.2708e-03
SCRBE n _A,p=20	1.6612e-05	1.2489e-04	4.7327e-04	1.2708e-03
$\widetilde \Delta $	1.4418e-06	2.0695e-07	7.9612e-08	9.6913e-08
$\widehat \Delta $	5.5488e-03	7.3845e-03	8.4207e-03	7.4811e-03
	λ ₅	λ ₆	λ ₇	λ ₈
Euler Bernoulli	—	2.9016e-03	5.6603e-03	—
Timoshenko	—	2.7622e-03	5.2991e-03	—
Global FEM	2.0732e-03	2.7775e-03	5.2916e-03	6.1912e-03
SCRBE n _A,p=108	2.0732e-03	2.7775e-03	5.2916e-03	6.1912e-03
SCRBE n _A,p=20	2.0732e-03	2.7775e-03	5.2916e-03	6.1912e-03
$\widetilde \Delta $	5.4576e-09	4.1418e-07	1.0262e-06	8.8249e-09
$\widehat \Delta $	3.3180e-02	8.3262e-03	8.9995e-03	4.7761e-03

The estimators $\widetilde \Delta $ and $\widehat \Delta $ correspond to relative errors. Note that we have eigenvalues of multiplicity two due to the symmetry of the beam square section but we only report distinct eigenvalues in this table.

We first observe that SCRBE does capture all the eigenvalues with their multiplicity: the eigenvalues corresponding to bending modes have double multiplicity because of the symmetry of the beam square section. We only report distinct eigenvalues in Table 1 but we show in Figure 4 the two non-collinear modes recovered by SCRBE for the first eigenvalue. Regarding the beam models (Euler Bernoulli and Timoshenko), we observe that they do not capture some eigenvalues; these correspond to torsional modes that are not taken into account in Euler Bernoulli and Timoshenko models which consider only bending displacement. Note that for a beam with a square section, the bending and torsion is decoupled and the eigenmodes are either pure bending or pure torsion (see Figure 5). For the modes that are pure bending (λ ₁, λ ₂, λ ₃, λ ₄, λ ₆, λ ₇), we observe a good agreement between all methods. Note that it is well known that Euler Bernoulli is better for long wavelength and/or slender beams; Timoshenko is better for shorter wavelength and/or shorter beams. Not surprisingly, the FE (and SCRBE) eigenvalues are closer to Euler Bernoulli for lower modes and closer to Timoshenko for higher modes. The SCRBE (with or without port reduction) and global FEM give results that have an actual relative difference less than 10⁻⁴. For the SCRBE without port reduction, we also give the relative error estimate $\widetilde \Delta $ in Table 1, which corresponds to the relative error between the SCRBE and the “truth” static condensation: it is at most 10⁻⁶, which confirms that the error introduced by RB is negligible. For the SCRBE with port reduction and n _A,p=20, the relative error estimate is $\widehat \Delta $ and corresponds to the relative error between SCRBE with and without port reduction: it is about 10⁻², which overestimates the actual relative error, but nonetheless indicates a very good agreement between SCRBE eigenvalues with and without port reduction. We also observe that the SCRBE does capture all the torsional modes. Note finally that the SCRBE eigenvalues are obtained using a root finding algorithm: in practice we set the tolerance^a to 10⁻¹⁰ as this is a couple orders of magnitude smaller than the RB relative error estimator $\widetilde {\Delta }$, thus making the root finding error negligible with respect to RB error (and also port reduction error).

Figure 4
Two non-collinear eigenmodes corresponding to the first eigenvalue of double multiplicity.

Figure 5
Eigenmodes for the fourth (pure bending) and fifth (pure torsion) eigenvalues.

Bridge structure

We are now ready to consider larger systems with more complicated connections which will better exercise the RB and port reduction capabilities. Towards this end, we consider a system of 30 components, corresponding to a bridge structure. It is composed of 22 beam components and 8 connectors, hence the vector of parameters μ for this system is of dimension 52.

We first set the vector of parameters μ such that E=0.5 and s=1 for all components, and we show in Figure 6 the second and third eigenmodes for the corresponding system. In the following, we will provide systematic analysis of the RB and port reduction convergence and also performance of the a posteriori error estimates.

We first show in Figure 7 the convergence of the first eigenvalue with respect to the size N of the RB spaces used for bubble approximations. Note that we did not compute the eigenvalue with the “truth” static condensation, because it would be very computationally intensive, hence the reference value for λ is the value obtained with a global FEM, denoted λ _FE ^b. We observe that we obtain exponential convergence, hence we provide a significant improvement compared to standard CMS approaches. We also observe that the RB relative error estimator $\widetilde {\Delta }$ is accurate – it overestimates the actual error by at most one order of magnitude; moreover, for a sufficiently large N, the RB relative error estimator $\widetilde {\Delta }$ is very small, hence justifying the fact that we can neglect the error due to RB error approximation when introducing port reduction.

Figure 6
A bridge structure: all of the “open ports” of beam components are clamped. The second and third displacement eigenmodes are shown.

Figure 7
First eigenvalue convergence with respect to the size N of RB spaces.

We now fix N=10 and consider port reduction. We show in Figure 8 the convergence of the first eigenvalue with respect to the number of port modes, for both the regular Laplacian modes and the empirical modes: the advantage obtained with the empirical modes is obvious, and we also observe that $\widehat \Delta $ does not converge as fast as the true error, which is due to the fact that it is only a linear function of the norm of the residual, as explained in Section ‘Port reduction error estimator’.

Figure 8
First eigenvalue convergence with respect to the number n _A,p of active port modes: blue corresponds to Laplacian eigenmodes (“Lap”), red corresponds to empirical modes (“Emp”). The reference eigenvalue $\widetilde \lambda $ is the one obtained for $n_{\text {A,p}}=\mathcal {N}_{p}^{\Gamma }=108$.

Finally, we briefly illustrate some component parametric variations made possible with SCRBE. We show in Figure 9 the third eigenmode for different parameter variations: we can modify some of the beam lengths (Figure 9a), or we can make one half of the bridge stiffer than the other (Figure 9b).

Figure 9
Illustration of some variations of the vector of parameters μ for the bridge system. We show the third eigenmode for two different configurations. **(a)** For the middle beams, s=0.7; for the beams adjacent to the middle beams, s=1.3; for all other beams and all support beams, s=1; and E=0.5 everywhere. **(b)** In the first half of the bridge E=2, in the second half E=0.5, and all the beams are of size s=1.

Industrial example

In this last section, we apply our approach to a large industrial structure. In the following, we will first focus on computational performance (without using the error estimators that have already been presented in the previous section), and then we will illustrate the parametric variability offered by our approach. Note that we will now consider linear elasticity in its dimensional form.

We consider here the shuttle part of a shiploader. A shiploader is a large structure (similar to a crane) used by mining companies to transport the minerals from trucks on the ground onto ships on the water. The shuttle is a subpart of the shiploader that can slide in and out, in order to vary the length and height of the structure, to accommodate for varying shapes and sizes of the incoming ships. The shuttle is comparable to the lattice boom of a crane, and has a frame structure composed of a series of intermeshing steel rods, reinforced with some panels on the sides. The shuttle structure is shown in Figures 10 and 12.

Figure 10
The shuttle structure (in the middle). Individual components used in our approach are showed separately around the assembled structure. Note that we instantiate the two truss components multiple times in order to assemble the shuttle structure.

The first goal of this section is to show the computational advantage of our method with respect to a classical Finite Element Method. The shuttle structure has a mesh composed of 430 000 nodes, and as a consequence the corresponding linear elasticity eigenproblem has 1.3 million degrees of freedom – we use first order elements and tetrahedral meshes. We show a part of the mesh for one of the components of the shuttle in Figure 11. For now, we consider the shuttle to be made of steel (Young’s modulus is 200 GPa and mass density is 7850 k g.m ⁻³) and we impose clamping in four shuttle locations (at the bottom, in the back and the middle of the structure) corresponding to the case where the shuttle would slide halfway out of the complete shiploader structure. These clamping locations are indicated by the “lock” icons in Figure 12, where we also show the displacement for the first and fifth eigenmodes.

Figure 11
The shuttle is clamped at the locations indicated by the locks in the left picture. The next two pictures correspond to the first and fifth computed eigenmodes: we show the displacements superimposed on a translucid view of the original structure.

Figure 12
The tetrahedral mesh for one component of the shuttle.

To solve the eigenproblem with SCRBE, we used RB spaces of dimension 20 on average for the bubble approximations, and we used on average 15 empirical modes for each port at which components connect. The final Schur system is of size 1200, to be compared with the size of the original FE system which is 1.3 million. We report in Table 2 the first five natural frequencies (square root of the eigenvalues) obtained both with FE and SCRBE. We observe a very good relative error of at most 2%, despite the dramatic dimension reduction performed by SCRBE. With respect to computational time, SCRBE improves on FE by a factor 700, which is very significant and allows for quasi real-time computations. Another important gain for SCRBE is on memory usage: it requires only 100 MB to solve an eigenproblem that requires 12 GB with FE. It means that very large structures that are out of reach for FE can be considered with SCRBE. For instance, if we were to consider the full shiploader, there would be about 6 millions degrees of freedom, and solving the eigenproblem with FE would not be possible on a regular desktop machine due to memory limitations, whereas it would be handled easily with SCRBE.

Table 2

Comparison between SCRBE and FE

	Global FEM	SCRBE	Relative error
Frequency 1	2.526 Hz	2.532 Hz	0.3%
Frequency 2	2.775 Hz	2.792 Hz	0.6%
Frequency 3	4.984 Hz	5.028 Hz	0.9%
Frequency 4	6.597 Hz	6.688 Hz	1.4%
Frequency 5	7.372 Hz	7.501 Hz	1.7%
RAM usage	12 GB	100 MB
Solving time	350 s	0.5 s

For the finite element eigen solver, we used the Krylov-Schur method with a shift and invert transformation, and the MUMPS [25] parallel sparse direct LU solver for matrix inversions, with 4 CPUs.

The second and most important goal of this section is to show the parametric advantage of our method with respect to CMS. We demonstrated that SCRBE has a computational advantage relative to FE, but the same decrease in computational time could in theory be obtained with CMS. One crucial advantage of SCRBE with respect to CMS (in addition to convergence rate) is its flexibility with respect to parameter variations. Thanks to the RB approximations at the component level, we can modify the component parameters and directly recompute the eigenproblem solution “Online”. In the case of CMS, any change of the component parameters (especially geometrical) would require some “Offline” work to recompute the modal decomposition of each component, hence precluding its use in a many query context with parametric variability. Although we did not implement the CMS method for direct comparison as we did for FE previously, we hope the following examples of Online parametric variations will convince the reader of the crucial advantage of SCRBE with respect to CMS.

We first describe the overall parametric variability of the shuttle assembly in Table 3 and Figure 13. Note that in the following we refer many times to “pre-bent” trusses: they correspond to components for which the geometry is bent in its initial state, as opposed to the bending shown with the eigenmode shapes. These pre-bent trusses can represent structures that have deformed over time, or in the case of buckling. The pre-bent truss component has two parameters v and h for vertical and horizontal pre-bending, and the mapping function for the pre-bending deformation reads

$$(x,y,z)\mapsto \left(x, y+v-\frac{vx^{2}}{l^{2}}, z+h-\frac{hx^{2}}{l^{2}}\right) $$

where the truss component is centered at the origin, has his main axis along the x coordinate, and is of length 2l.

Figure 13
Horizontal truss with pre-bending geometrical variability. Left: horizontal pre-bending. Right: vertical pre-bending.

Table 3

The parametric variability of each component used in the shuttle assembly

Component type	Number of parameters	Parameters and ranges
		Young’s modulus (frame, panel) ∈[60,220]G P a
Side panel	4	Mass density (frame, panel) ∈[1000,8000]k g.m ⁻³
		Young’s modulus ∈[60,220]G P a
Truss joint	2	Mass density ∈[1000,8000]k g.m ⁻³
		Young’s modulus ∈[60,220]G P a
Diagonal truss	4	Mass density ∈[1000,8000]k g.m ⁻³
		Length, shear
		Young’s modulus ∈[60,220]G P a
		Mass density ∈[1000,8000]k g.m ⁻³
		Vertical pre-bending v∈[−1.5,1.5]
Horizontal truss	4	Horizontal pre-bending h∈[−1,1]

In total, the full shuttle has a vector of parameters μ of dimension 136.

In total, the shuttle has 122 material parameters (Young’s modulus and mass densities) and 14 geometrical parameters (horizontal and vertical pre-bending of the horizontal trusses) that can be varied independently – the vector of parameters μ for this system is of dimension 136. We report in Table 4 the first and fifth natural frequencies of the shuttle for various choices of parameters.

Table 4

The first and fifth natural frequencies of the shuttle for various configurations

Shuttle configuration	First natural frequency	Fifth natural frequency
Pristine, all steel	2.53 Hz	7.50 Hz
Pristine, steel frame, aluminium panels	3.13 Hz	8.10 Hz
Pristine, all aluminium	2.54 Hz	7.51 Hz
Pre-bent trusses, all steel	2.53 Hz	7.07 Hz

For steel, the Young’s modulus is 200 GPa and the mass density is 750 k g.m ⁻³. For aluminium, the Young’s modulus is 69 GPa and the mass density is 2700 k g.m ⁻³. For the pre-bent trusses case, we used maximal horizontal and vertical pre-bending parameters for all the horizontal trusses.

We observe almost no change in the frequencies when the shuttle is either all steel or all aluminium. This is because the homogeneous Young modulus and mass density can be factored out of the stiffness and mass matrices, and the ratio between these two quantities is almost the same for steel and aluminium. On the opposite, if we mix both materials, as in the case of a steel frame and aluminium panels, then the natural frequencies significantly change. Now if we pre-bend the horizontal trusses, we observe that the first frequency is unchanged whereas the fifth frequency is affected. This is because the first eigenmode corresponds to a bending along the principal axis of the shuttle, and does not involve any deformation of the horizontal trusses, whereas the fifth eigenmode corresponds to a lateral bending which involves some horizontal trusses (see Figure 12).

Using CMS, we could still vary some material parameters (if homogeneous at the component level) but we could not vary geometrical parameters of a given component “Online”. Regarding the previous examples, we could probably switch from all steel to all aluminium with CMS without affecting much the accuracy (and the natural frequencies would not change much anyway), but the two other cases would not be possible without some new “Offline” computations. In order to better illustrate the geometrical variability offered by the SCRBE method, we will consider the pre-bent truss component in isolation from the rest of the shuttle, since the full shuttle structure is not much affected by a local geometrical variation. We show in Figure 14 an assembly of two pre-bent trusses clamped on both sides, for various geometrical parameters, and we report in Table 5 the first natural frequency computed both with SCRBE and FE. We can see that the SCRBE method captures very well the first natural frequency despite large geometrical variations.

Figure 14
A system composed of two pre-bent truss components, clamped on both extremities. The geometrical parameters are varied, from left to right: no pre-bending, horizontal pre-bending, vertical pre-bending, simultaneous horizontal and vertical pre-bending.

Table 5

The first natural frequency for the system composed of two pre-bent truss components (steel)

	No pre-bending	Horizontal pre-bending	Vertical pre-bending	Horizontal and vertical
				pre-bending
SCRBE	12.608 Hz	11.868 Hz	12.246 Hz	11.553 Hz
FE	12.606 Hz	11.852 Hz	12.241 Hz	11.534 Hz

Conclusions

We extended the SCRBE approach – originally introduced for parametrized linear problems – to parametrized symmetric eigenproblems, in order to analyze large-scale component-based structures. Thanks to the component-interior reduced basis and the port reduction, we are able to compute fast accurate approximations for any component parameter values, as well as providing a posteriori error estimates.

We presented an application to a large structure – a shiploader shuttle used in mining – in the context of three-dimensional linear elasticity. Compared to a finite element method, we obtain a speed up of 700 and a reduction of 120 in memory consumption. We are also able to explore the parametric variability of the shuttle – a vector μ of dimension 136 – and recompute the solution at the same speed for every new value of μ.

We obviously presented a limited number of cases, but the parametric variability of the shuttle, to which we can add variable clamping conditions, allows to consider thousands of designs, and in very little time thanks to the computational speed of SCRBE. Moreover, the small memory requirements of the method would allow to consider even larger structure, such as a full shiploader model. For these reasons we think our method can be very valuable in an engineering context where design optimization and multi-scenario analysis of large models is common practice.

Endnotes

^a The tolerance applies to $\widetilde {\overline {\tau }}_{n}(\mu,\sigma)=0$, hence it corresponds to a relative tolerance for $\widetilde {\lambda }_{n}(\mu)$.

^b The global FEM eigenvalue is not expected to be exactly the same as what would be obtained with FE static condensation – in theory they should be the same, but the different computational paths lead to different numerical results – hence it explains why $\frac {|\lambda _{\textit {FE}}-\widetilde {\lambda }|}{\lambda _{\textit {FE}}}$ does not converge to zero, and why $\widetilde {\Delta }$ gets smaller than $\frac {|\lambda _{\textit {FE}}-\widetilde {\lambda }|}{\lambda _{\textit {FE}}}$ for N big enough.

Appendix A

Properties used for error estimates

Hypothesis A.1.

σ=λ _n(μ) if and only if $\overline {{\tau }}_{n}(\mu,\sigma) = 0$

Lemma A.1.

We have that

$$ \frac{\partial\tau_{n}(\mu,\sigma)}{\partial \sigma} = -\frac{1}{\lambda_{n}(\mu)}, $$

(57)

for each $n=1,2,\ldots,\mathcal {N}$.

Proof.

We set v=χ _n(μ) in (3), to obtain

$$ \mathcal{B}(\chi_{n}(\mu),\chi_{n}(\mu);\mu;\sigma) = \tau_{n}(\mu,\sigma)a(\chi_{n}(\mu),\chi_{n}(\mu);\mu) = \tau_{n}(\mu,\sigma), $$

(58)

where we employed (4) in the last equality above. We note that χ _n(μ) is independent of σ, and differentiate with respect to σ to obtain

$$\begin{array}{@{}rcl@{}} \frac{\partial\tau_{n}(\mu,\sigma)}{\partial \sigma} &=& \frac{\partial}{\partial \sigma} \mathcal{B}(\chi_{n}(\mu),\chi_{n}(\mu);\mu;\sigma)\\ &=& \frac{\partial}{\partial \sigma}\left[ a(\chi_{n}(\mu),\chi_{n}(\mu);\mu) - \sigma m(\chi_{n}(\mu),\chi_{n}(\mu);\mu) \right]\\ &=& -m(\chi_{n}(\mu),\chi_{n}(\mu);\mu)\\ &=& -\frac{1}{\lambda_{n}(\mu)}m(u_{n}(\mu),u_{n}(\mu);\mu) = -\frac{1}{\lambda_{n}(\mu)}. \end{array} $$

However, the result does not apply to $\overline {\tau }_{n}(\mu,\sigma)$: we cannot apply the argument from the proposition to (21), (22) since in general $\overline {\chi }_{n}(\mu,\sigma)$ depends on σ. We can still state the following

Proposition A.1.

Assuming that $\overline {\tau }_{n}(\mu,\cdot)$is differentiable at λ _n(μ)and Hypothesis A.1 holds, then

$$\frac{\partial\overline{\tau}_{n}(\mu,\lambda_{n})}{\partial \sigma} = -\frac{1}{\lambda_{n}(\mu)}. $$

Proof.

We know that $\overline {\tau }_{n}(\mu,\lambda _{n}(\mu))=\tau _{n}(\mu,\lambda _{n}(\mu))=0,\quad \frac {\partial \tau _{n}(\mu,\sigma)}{\partial \sigma } = -\frac {1}{\lambda _{n}(\mu)}$ and $\overline {\tau }_{n}(\mu,\sigma) \geq \tau _{n}(\mu,\sigma)$. So we have

$$\forall h<0,\quad \frac{\overline{\tau}_{n}(\mu,\lambda_{n}(\mu)+h)}{h}\leq -\frac{1}{\lambda_{n}(\mu)},$$

$$\forall h>0,\quad \frac{\overline{\tau}_{n}(\mu,\lambda_{n}(\mu)+h)}{h}\geq -\frac{1}{\lambda_{n}(\mu)},$$

Since $\overline {\tau }_{n}(\mu,\cdot)$ is differentiable at λ _n(μ), we have

$$\frac{\partial\overline{\tau}_{n}(\mu,\lambda_{n}(\mu))}{\partial \sigma} = {\lim}_{h\rightarrow 0^{-}}\frac{\overline{\tau}_{n}(\mu,\lambda_{n}(\mu)+h)}{h}={\lim}_{h\rightarrow 0^{+}}\frac{\overline{\tau}_{n}(\mu,\lambda_{n}(\mu)+h)}{h}=-\frac{1}{\lambda_{n}(\mu)}. $$

Declarations

Acknowledgements

This work was supported by OSD/AFOSR/MURI Grant FA9550-09-1-0613, by ONR Grant N00014-11-1-0713, and by a grant from the MIT Deshpande Center for Technological Innovation. This work was also supported by the Commission for Technology and Innovation CTI of the Swiss Confederation.

Authors’ Affiliations

(1)

Massachusetts Institute of Technology

(2)

Harvard University

(3)

Akselos, EPFL Innovation Park

(4)

Swiss Federal Institute of Technology in Lausanne

References

Craig R, Bampton M (1968) Coupling of substructures for dynamic analyses. AIAA J 6(7): 1313–1319.MATHView ArticleGoogle Scholar
Hurty WC (1965) Dynamic analysis of structural systems using component modes. AIAA J 3(4): 678–685.View ArticleGoogle Scholar
Maday Y, Rønquist EM (2002) A reduced-basis element method. J Sci Comput 17(1): 447–459.MATHMathSciNetView ArticleGoogle Scholar
Rozza G, Huynh DBP, Patera AT (2008) Reduced basis approximation and a posteriori error estimation for affinely parametrized elliptic coercive partial differential equations. Arch Comput Methods Eng 15(3): 229–275.MATHMathSciNetView ArticleGoogle Scholar
DeVore R, Petrova G, Wojtaszczyk P (2013) Greedy algorithms for reduced bases in banach spaces. Constructive Approximation 37(3): 455–466.MATHMathSciNetView ArticleGoogle Scholar
Iapichino L, Quarteroni A, Rozza G (2012) A reduced basis hybrid method for the coupling of parametrized domains represented by fluidic networks. Comput Methods Appl Mech Eng 221: 63–82.MathSciNetView ArticleGoogle Scholar
Maier I, Haasdonk B (2014) A dirichlet–neumann reduced basis method for homogeneous domain decomposition problems. Appl Numerical Math 78: 31–48.MATHMathSciNetView ArticleGoogle Scholar
Nguyen NC (2008) A multiscale reduced-basis method for parametrized elliptic partial differential equations with multiple scales. J Comput Phys 227(23): 9807–9822.MATHMathSciNetView ArticleGoogle Scholar
Efendiev Y, Galvis J, Hou TY (2013) Generalized multiscale finite element methods (gmsfem). J Comput Phys 251: 116–135.MathSciNetView ArticleGoogle Scholar
Huynh D, Knezevic D, Patera A (2013) A static condensation reduced basis element method: Approximation and a posteriori error estimation. ESAIM: Math Model Numerical Anal 47(1): 213–251.MATHMathSciNetView ArticleGoogle Scholar
Bourquin F (1992) Component mode synthesis and eigenvalues of second order operators: discretization and algorithm. Modélisation Mathématique et Analyse Numérique 26(3): 385–423.MATHMathSciNetGoogle Scholar
Charpentier I, De Vuyst F, Maday Y (1996) A component mode synthesis method of infinite order of accuracy using subdomain overlapping: numerical analysis and experiments. Publication du laboratoire d’Analyse Numerique R 96002: 55–65.Google Scholar
Hetmaniuk UL, Lehoucq RB (2010) A special finite element method based on component mode synthesis. ESAIM: Math Model Numerical Anal 44(03): 401–420.MATHMathSciNetView ArticleGoogle Scholar
Isaacson E, Keller H (1994) Computation of eigenvalues and eigenvectors, analysis of numerical methods.Google Scholar
Bermúdez A, Pena F (2011) Galerkin lumped parameter methods for transient problems. Int J Numerical Methods Eng 87(10): 943–961.MATHView ArticleGoogle Scholar
Eftang JL, Patera AT (2013) Port reduction in parametrized component static condensation: approximation and a posteriori error estimation. Int J Numerical Methods Eng 96(5): 269–302.MathSciNetGoogle Scholar
Courant R, Hilbert D (1953) Methods of mathematical physics, vol. 1. Interscience Publishers Inc., New York, NY, USA.Google Scholar
Huynh DBP, Rozza G, Sen S, Patera AT (2007) A successive constraint linear optimization method for lower bounds of parametric coercivity and inf-sup stability constants. Comptes Rendus Math 345(8): 473–478.MATHMathSciNetView ArticleGoogle Scholar
Kunisch K, Volkwein S (2002) Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics. SIAM J Numerical Anal 40(2): 492–515.MATHMathSciNetView ArticleGoogle Scholar
Weinberger H (1974) Variational methods for eigenvalue approximation, Vol. 15. SIAM, Philadelphia, PA, USA.MATHView ArticleGoogle Scholar
Brent RP (1973) Algorithms for minimization without derivatives. Courier Dover Publications, Mineola, NY, USA.MATHGoogle Scholar
Hernandez V, Roman JE, Vidal V (2005) SLEPc: A scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans Math Softw 31(3): 351–362.MATHMathSciNetView ArticleGoogle Scholar
Prud’homme C, Rovas D, Veroy K, Maday Y, Patera A, Turinici G (2002) Reliable real-time solution of parametrized partial differential equations: Reduced-basis output bounds methods. J Fluids Eng 124(1): 70–80.View ArticleGoogle Scholar
Timoshenko S (1937) Vibration Problems in Engineering. D.Van Nostrand Company Inc., New York, NY, USA.MATHGoogle Scholar
Amestoy PR, Guermouche A, L’Excellent J-Y, Pralet S (2006) Hybrid scheduling for the parallel solution of linear systems. Parallel Comput 32(2): 136–156.MathSciNetView ArticleGoogle Scholar

Copyright

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.