- Research article
- Open access
- Published:
A hybrid interface preconditioner for monolithic fluid–structure interaction solvers
Advanced Modeling and Simulation in Engineering Sciences volume 7, Article number: 15 (2020)
Abstract
We propose a hybrid interface preconditioner for the monolithic solution of surface-coupled problems. Powerful preconditioning techniques are crucial when it comes to solving large monolithic systems of linear equations efficiently, especially when arising from coupled multi-physics problems like in fluid–structure interaction. Existing physics-based block preconditioners have proven to be efficient, but their error assessment reveals an accumulation of the error at the coupling surface. We address this issue by combining them with an additional additive Schwarz preconditioner, whose subdomains span across the interface on purpose. By performing cheap but accurate subdomain solves that do not depend on the separation of physical fields, this error accumulation can be reduced effectively. Numerical experiments compare the performance of the hybrid preconditioner to existing approaches, demonstrate the increased efficiency, and study its parallel performance.
Introduction
In this paper, we propose a novel preconditioner for the monolithic solution of surface-coupled multi-physics problems. A prominent representative of surface-coupled problems is the interaction of a fluid flow with solid bodies undergoing large deformation, which is commonly referred to as fluid–structure interaction (FSI). In a wide range of FSI applications, monolithic solvers as described in e.g. [1] were found to be a suitable solution strategy, in particular in scenarios that are prone to the artificial added mass effect [2,3,4,5]. Monolithic solvers most often address the nonlinearity with a Newton scheme [1, 6,7,8,9,10,11]. Within the usually applied Krylov solver—most often the Generalized Minimal Residual (GMRES) method [12]—a good preconditioner is crucial for an efficient solution process. As the system matrix exhibits a block structure, that is closely related to the involved solid, fluid, and fluid mesh motion fields, preconditioners have been designed that exploit this particular block structure of the monolithic system matrix. They are often referred to as physics-based block preconditioners. Such preconditioners can conveniently be constructed from single-field preconditioners such as algebraic multigrid (AMG) methods [13, 14]. However, physics-based block preconditioning of surface-coupled problems exhibits an accumulation of the error at the coupling surface. These errors primarily have to be addressed by the outer Krylov method. We demonstrate this numerically and by means of an error assessment. Since such preconditioners are build on the separation of physical fields by the coupling surface, they cannot deliver smoothness of the solution across the interface (see also [6]). The proposed preconditioner aims at reducing exactly these accumulated errors at the interface and accelerating the overall solution process.
We address this issue with a novel hybrid interface preconditioner that combines the multigrid performance of existing physics-based block preconditioners with an additional interfacial Schwarz preconditioner. The latter one is constructed based on an overlapping domain decomposition, whose subdomains intentionally span across the fluid-structure interface. By using subdomain solvers that are insensitive to the separation of physics by the interface a high-quality solution can be obtained. In combination with the physics-based block preconditioners, the error accumulation at the interface can be reduced effectively yielding reductions in iteration counts and total time to solution.
A variety of physics-based block preconditioning approaches has been reported in literature. Gee et al. [6] proposed physics-based block preconditioners by combining AMG methods and block Gauß–Seidel (BGS) methods. An algorithmic modification, where the BGS method is replaced by an approximate Schur complement, is described by Langer and Yang [15] and has been extended to a fully parallel framework by Jodlbauer et al. [16]. Starting from the ideas in [6], an extension to the monolithic coupling of an arbitrary number of fields is detailed in [17]. An open-source implementation by Wiesner et al. [18] makes such block AMG preconditioners available via the MueLu package [19, 20] of the Trilinos library.Footnote 1 Heil [7] and Heil et al. [4] use block-triangular approximations to the full Jacobian as preconditioner. A preconditioner based on pseudo-solid mesh updates is proposed and analyzed by Muddle et al. [21]. Several preconditioner designs are briefly sketched by Tezduyar and Sathe [11] in the context of space-time finite elements. By extending the work of Crosetto et al. [22], a block preconditioner for the factorized and statically condensed FSI matrix with a SIMPLE preconditioner for the fluid subproblem has recently been proposed by Deparis et al. [23].
To assess the performance gains, that can be achieved by the novel preconditioner, we study large-scale three-dimensional FSI examples. We analyze the solver performance with ongoing mesh refinement and increasing numbers of processors. As reference solver, we compare our preconditioner to the AMG-based preconditioners proposed in [6] on FSI problems only. However, we stress that the proposed methodology is not limited to specific FSI preconditioners, but can rather be seen as a general framework that reduces error accumulation at the interface for any physics-based block preconditioner for surface-coupled problems. Besides FSI, contact mechanics or the transport of a scalar species through a membrane pose promising applications for such a preconditioner.
The remainder of this manuscript is organized as follows: After a brief introduction to the underlying FSI formulation and the monolithic solution scheme in “Fluid–structure interaction in a Nutshell” section, existing physics-based AMG block preconditioning techniques tailored to FSI problems are briefly reviewed in “Physics-based block preconditioning tailored to fluid–structure interaction” section. In “Hybrid interface preconditioner for surface-coupled problems” section, we propose the novel hybrid interface preconditioner and detail its requirements, setup, and application. Extensive numerical experiments are reported in “Numerical experiments” section, where the presented methods are compared to each other and performance and efficiency are assessed in terms of iterations and timings. Mesh refinement studies and simulations on large numbers of cores are shown. Finally, we summarize our work in “Concluding remarks and outlook” section. Appendix A briefly outlines our strategy to check for convergence of the iterative linear and nonlinear solvers in case of a monolithic solution framework.
Fluid–structure interaction in a Nutshell
The FSI problem considered here consists of an incompressible fluid flow described in an arbitrary Lagrangean–Eulerian (ALE) description which interacts with a solid body undergoing large deformation. Adopted from our work on time step size adaptivity [24] for FSI solvers, a only brief introduction to such fluid–structure interaction problems is given, while a detailed description of the model, its discretization, and a thorough derivation of the monolithic solution method have been presented by Mayr et al. [1].
Physical model
We couple two physical domains, namely a deformable fluid domain  and a solid domain
and a solid domain  , cf. Fig. 1.
, cf. Fig. 1.
Problem statement adopted from [25]—Left: The domain \(\Omega \) is subdivided into a fluid domain  and a structural domain
and a structural domain  by the fluid-structure interface \(\Gamma _\mathrm {FSI}\). Both subdomains are bounded by Dirichlet boundaries
by the fluid-structure interface \(\Gamma _\mathrm {FSI}\). Both subdomains are bounded by Dirichlet boundaries  and
and  , Neumann boundaries
, Neumann boundaries  and
and  , and the common fluid-structure interface \(\Gamma _\mathrm {FSI}\), respectively. Right: At the interface, kinematic continuity as well as equilibrium of interface traction fields
, and the common fluid-structure interface \(\Gamma _\mathrm {FSI}\), respectively. Right: At the interface, kinematic continuity as well as equilibrium of interface traction fields  and
and  are required
are required
To account for the moving fluid domain, an ALE observer is used for the fluid field, while the solid body is described in a purely Lagrangean fashion. The fluid field is governed by the incompressible Navier–Stokes equations

with the primary unknowns  and
and  being the fluid velocity and pressure field, respectively. The fluid density and dynamic viscosity are denoted by
being the fluid velocity and pressure field, respectively. The fluid density and dynamic viscosity are denoted by  and
and  , respectively, while the strain rate tensor is computed as the symmetric gradient of the fluid velocity
, respectively, while the strain rate tensor is computed as the symmetric gradient of the fluid velocity  . Body forces in the fluid field are denoted by
. Body forces in the fluid field are denoted by  . As the fluid field is described in an ALE fashion, the grid velocity
. As the fluid field is described in an ALE fashion, the grid velocity  needs to be computed from the grid displacement field
needs to be computed from the grid displacement field  . For moderately deforming fluid domains, the grid displacement field
. For moderately deforming fluid domains, the grid displacement field  is determined by harmonic extension whereas large deformations require the assumption that the ALE field behaves like a pseudo-elastic solid. The solid body with density \(\rho ^{\mathscr {S}}\) and body force
is determined by harmonic extension whereas large deformations require the assumption that the ALE field behaves like a pseudo-elastic solid. The solid body with density \(\rho ^{\mathscr {S}}\) and body force  per undeformed unit volume is governed by the balance of linear momentum
per undeformed unit volume is governed by the balance of linear momentum

where the displacement field  is the primary unknown. In this work, we assume a hyperelastic strain energy function
is the primary unknown. In this work, we assume a hyperelastic strain energy function  to compute the 2nd Piola–Kirchhoff stresses
to compute the 2nd Piola–Kirchhoff stresses  using the right Cauchy–Green tensor
using the right Cauchy–Green tensor  with
with  being the solid’s deformation gradient. At the fluid-structure interface \(\Gamma _\mathrm {FSI}\), we require kinematic continuity of fluid and solid velocity fields, i.e.
being the solid’s deformation gradient. At the fluid-structure interface \(\Gamma _\mathrm {FSI}\), we require kinematic continuity of fluid and solid velocity fields, i.e.  , as well as equilibrium of interface traction fields
, as well as equilibrium of interface traction fields  and
and  with
with  referring to the fluid domain’s deformation gradient and
referring to the fluid domain’s deformation gradient and  and
and  denoting the outward unit normal vector of the fluid and solid domain in the undeformed configuration, respectively. The kinematic constraint is enforced weakly via a Lagrange multiplier field \(\underline{\mathbf {\varvec{\lambda }}}\), which allows for an interpretation of the Lagrange multiplier field as the interface traction that acts onto the solid side of the interface, reading
denoting the outward unit normal vector of the fluid and solid domain in the undeformed configuration, respectively. The kinematic constraint is enforced weakly via a Lagrange multiplier field \(\underline{\mathbf {\varvec{\lambda }}}\), which allows for an interpretation of the Lagrange multiplier field as the interface traction that acts onto the solid side of the interface, reading  .
.
The monolithic solution method for FSI
To establish a monolithic solution method for the coupled FSI problem, where all equations are solved simultaneously, spatial and temporal discretization is performed field-wise before the final assembly of the monolithic system of equations. For the spatial discretization of the solid and the fluid field, we employ the finite element method. In the solid field, displacement-based first-order Lagrangean finite elements are utilized, while techniques to deal with locking phenomena can be employed where necessary. In the fluid field, equal-order interpolated finite elements are used that require residual-based stabilization like Streamline Upwind Petrov–Galerkin (SUPG) [26], Pressure-Stabilized Petrov–Galerkin (PSPG) [27], and a grad-div term [28]. The stabilization parameter follows the definition by [29]. The Lagrange multiplier field is discretized with a dual mortar method [30, 31] that results in mortar coupling matrices that allow for a cheap condensation of the Lagrange multiplier degrees of freedom from the monolithic system of equations. In the context of mortar methods, either the solid or the fluid field can be chosen as the master side, resulting in two distinct solver formulations, cf. Mayr et al. [1] for details. Time discretization is based on finite differencing and allows for an independent choice of the time integration schemes in the solid and the fluid field in a temporally consistent manner [1] with the possibility to control temporal accuracy via an adaptive time stepping scheme based on a posteriori error estimation, cf. Mayr et al. [24].
Putting the residual expressions  ,
,  and
and  from the solid, the ALE, and the fluid field as well as the kinematic constraint \(\mathbf {r}^{\mathrm {coupl}}\) together yields the monolithic nonlinear residual vector
from the solid, the ALE, and the fluid field as well as the kinematic constraint \(\mathbf {r}^{\mathrm {coupl}}\) together yields the monolithic nonlinear residual vector  that needs to vanish in every time step. The nonlinearity is treated by a Newton–Krylov method. The outer Newton loop address the nonlinear character of the FSI problem and requires the consistent linearization of the residual vector \(\mathbf {r}^{\mathrm {FSI}}\) in order to setup a linear problem to compute the Newton step increment \(\Delta \mathbf {x}\). Each linear system is then solved using a Krylov subspace method, in particular preconditioned GMRES [12]. The preconditioners are tailored to the physics-based block structure of the FSI system matrix and are detailed in “Physics-based block preconditioning tailored to fluid–structure interaction” and “Hybrid interface preconditioner for surface-coupled problems” sections. Further details are given in our previous work [1, 6], while others also use similar approaches [10, 23].
that needs to vanish in every time step. The nonlinearity is treated by a Newton–Krylov method. The outer Newton loop address the nonlinear character of the FSI problem and requires the consistent linearization of the residual vector \(\mathbf {r}^{\mathrm {FSI}}\) in order to setup a linear problem to compute the Newton step increment \(\Delta \mathbf {x}\). Each linear system is then solved using a Krylov subspace method, in particular preconditioned GMRES [12]. The preconditioners are tailored to the physics-based block structure of the FSI system matrix and are detailed in “Physics-based block preconditioning tailored to fluid–structure interaction” and “Hybrid interface preconditioner for surface-coupled problems” sections. Further details are given in our previous work [1, 6], while others also use similar approaches [10, 23].
After assembly, consistent linearization, and subsequent static condensation of the Lagrange multiplier and slave side interface degrees of freedom, the monolithic system of linear equations schematically reads

The matrices  ,
,  , and
, and  on the main diagonal reflect the solid, the ALE, and the fluid field residual linearizations, respectively. The coupling among the fields is represented by the off-diagonal blocks
on the main diagonal reflect the solid, the ALE, and the fluid field residual linearizations, respectively. The coupling among the fields is represented by the off-diagonal blocks  , where superscripts
, where superscripts  indicate the coupling between the fields. Note the arrow-shaped structure of the matrix, that lays the foundation for the development of physics-based block preconditioners. A practical strategy to check for convergence of the linear and nonlinear iterative solver in case of monolithic approaches is outlined in Appendix A section.
indicate the coupling between the fields. Note the arrow-shaped structure of the matrix, that lays the foundation for the development of physics-based block preconditioners. A practical strategy to check for convergence of the linear and nonlinear iterative solver in case of monolithic approaches is outlined in Appendix A section.
Physics-based block preconditioning tailored to fluid–structure interaction
A variety of preconditioners for block matrices as given in (1) is available in literature. Common to all these approaches is that they exploit the block structure of the system matrix. The block structure usually corresponds to the grouping of the unknowns of the different physical fields, while the coupling between the fields is reflected by the off-diagonal blocks. Thus, such preconditioners are often referred to as physics-based block preconditioners. Two particular AMG-based approaches from [6] are summarized briefly, because they will be used as baseline preconditioners to which the proposed interface preconditioner is applied and compared.
A block-iterative approach with internal algebraic Multigrid preconditioners
A block version of the Gauß–Seidel method, referred to as block Gauß–Seidel (BGS), can be used as preconditioner for the monolithic system of equations (1). It can be achieved by dropping the upper-triangular coupling blocks in (1), yielding the forward BGS preconditioner

For efficiency and scalability, the block inverses  ,
,  , and
, and  are approximated by preconditioning operations
are approximated by preconditioning operations  ,
,  , and
, and  based on AMG hierarchies tailored to each field. Since this preconditioner uses a BGS method on the outside with embedded AMG preconditioners for each physical field, it is denoted by BGS(AMG).
based on AMG hierarchies tailored to each field. Since this preconditioner uses a BGS method on the outside with embedded AMG preconditioners for each physical field, it is denoted by BGS(AMG).
Obviously, even if the block inverses can be computed exactly, the error after one application of the preconditioner concentrates at the fluid-structure interface since the interface is only treated by the less powerful BGS method. To reduce those errors, quite some additional Krylov iterations need to be performed. This is expensive, especially in the context, that one needs to deal with the full system just to reduce the error in a small, but important portion of it.
A fully coupled algebraic Multigrid preconditioner
Assuming the existence of field-specific multigrid restriction operators  ,
,  , and
, and  as well as prolongation operators
as well as prolongation operators  ,
,  , and
, and  associated with the level transfer between levels \(\ell \) and \(\ell +1\) for solid, ALE, and fluid field, respectively, a representation of the monolithic system of linear equations is constructed on every level \(\ell \in [0,n^{\ell }-1]\) with \(n^{\ell }\) being the number of levels of the multigrid hierarchy. It consists of the coarsened Jacobian matrix
associated with the level transfer between levels \(\ell \) and \(\ell +1\) for solid, ALE, and fluid field, respectively, a representation of the monolithic system of linear equations is constructed on every level \(\ell \in [0,n^{\ell }-1]\) with \(n^{\ell }\) being the number of levels of the multigrid hierarchy. It consists of the coarsened Jacobian matrix

while the residual vector \({\mathbf {r}_{\ell +1}}\) is computed as restriction of the fine level residual vector, reading

FSI-specific block methods are applied on each level of the fully coupled AMG hierarchy. This strongly enhances the preconditioning effect, since interface-related errors can be tackled by the coarse grid correction effectively. On fine and medium levels, the BGS method (2) is applied, while the actions of the block inverses are approximated with the same field-specific one-level preconditioners, that already have been used as level smoothers in the internal AMG hierarchies of the BGS(AMG) approach. On the coarse level, usually a BGS(LU), i.e. a block Gauß–Seidel method with exact block inverses, is preferred over a direct solve on the fully coupled coarse level matrix to avoid the assembly into a single sparse matrix. Since the FSI coupling terms are incorporated on the coarse levels \(\ell >0\), this approach is referred to as fully coupled algebraic multigrid preconditioner and is denoted by AMG(BGS).
Following the arguments in [6] when comparing the fully-coupled AMG preconditioner to the block-iterative approach from “A block-iterative approach with internal algebraic multigrid preconditioners” section, a certain amount of improvement can be expected, since the interface coupling is transferred to the multigrid coarse levels and, thus, the coarse level corrections reflect the interface coupling. However, the basic issue of a block preconditioner that relies on the physics-based block structure of the matrix is still present. Thinking in terms of AMG(BGS), the fine and coarse level coupling is still only addressed by means of the BGS method, even if the block inverses inside the BGS method are computed exactly. Hence, a concentration of error at the fluid-structure interface is still expected, even if it is less pronounced as for the BGS(AMG) approach.
Remark 1
Physics-based block preconditioners are often implemented in a parallel setting with distributed data based on a domain decomposition that respects the boundaries of the physical fields (see [6, 7, 15, 16, 23] for example). Therefore, the computational domain \(\Omega \) is partitioned into the solid domain  and the fluid domain
and the fluid domain  . Afterwards, an overlapping domain decomposition is generated for each physical subdomain
. Afterwards, an overlapping domain decomposition is generated for each physical subdomain  and
and  and distributed among all parallel processes involved. As a result, subdomain boundaries coincide with the fluid-structure interface \(\Gamma _\mathrm {FSI}\). However, the partitioning of
and distributed among all parallel processes involved. As a result, subdomain boundaries coincide with the fluid-structure interface \(\Gamma _\mathrm {FSI}\). However, the partitioning of  and
and  does not necessarily match at \(\Gamma _\mathrm {FSI}\) as will be detailed in “Partitioning and setup of the domain decomposition” section.
does not necessarily match at \(\Gamma _\mathrm {FSI}\) as will be detailed in “Partitioning and setup of the domain decomposition” section.
Error assessment for physics-based block preconditioners
To lay the foundation for a later analysis of the proposed preconditioner, we now study the error matrices and error propagation associated with such physics-based block preconditioners. In general, the error matrix is given as

with  being the Jacobian matrix from (1) and \(\varvec{\mathscr {M}}\) denoting the preconditioner to be studied. By multiplying (4) with
being the Jacobian matrix from (1) and \(\varvec{\mathscr {M}}\) denoting the preconditioner to be studied. By multiplying (4) with  from the left, the error propagation operator
from the left, the error propagation operator  is obtained as
is obtained as

with \(\mathbf {I}\) denoting identity.
To gain detailed insight, we further split each vector of unknowns into interior and interface degrees of freedom, denoted by subscripts \(\left( \bullet \right) _{\mathrm {I}}\) and \(\left( \bullet \right) _{\Gamma }\), respectively. Interface degrees of freedom are associated with nodes located at the fluid-structure interface, while interior degrees of freedom represent nodes that reside in the interior of the solid, fluid, and ALE domain. Exemplarily, we study the case of fluid-handled interface motion as introduced in [1], where the interface motion is solely represented by fluid field unknowns, while the solid and ALE interface degrees of freedom have been condensed along with the Lagrange multiplier unknowns. Then, the Jacobian matrix and an exemplary BGS preconditioner \(\varvec{\mathscr {M}}_{\mathrm {BGS}}\) yield the error matrix

The non-zero blocks in  are associated with the FSI interface coupling terms of
are associated with the FSI interface coupling terms of  , clearly demonstrating the error accumulation at the fluid-structure interface. When assuming exact block inverses, the error propagation for the forward BGS preconditioner reads
, clearly demonstrating the error accumulation at the fluid-structure interface. When assuming exact block inverses, the error propagation for the forward BGS preconditioner reads

with the Schur complement

As a consequence of (6), the error propagation vanishes at all interior degrees of freedom \(\left( \bullet \right) _{\mathrm {I}}\) of all three fields, but does not vanish at the fluid-structure interface.
For the sake of brevity, the respective analysis for a fully coupled AMG preconditioner with BGS level smoothers described in “A fully coupled algebraic multigrid preconditioner” section is not shown here, since it follows exactly the same line of argument and the key result is the same.
Hybrid interface preconditioner for surface-coupled problems
Both preconditioning approaches presented in “Physics-based block preconditioning tailored to fluid–structure interaction” section exploit the block structure of the FSI system matrix, that is related to the separation of physical fields by the fluid-structure interface. A commonality of all physics-based block preconditioners is the concentration of error at the coupling surface as already indicated at the end of “A block-iterative approach with internal algebraic multigrid preconditioners” section. The present section aims at particularly addressing this issue. The goal of reducing the error at the coupling surface can be achieved by combining the existing physics-based block preconditioners with an additional interface preconditioner that is based on a purposely ’non-physics-based’ overlapping domain decomposition. By neglecting the location of the interface when generating the parallel domain decomposition, the resulting subdomains span across the fluid-structure interface on purpose. The use of high-quality solves, i.e. direct or close-to-direct solves, on the patches across the interface reduces the accumulated error stemming from the physics-based block preconditioner effectively. Of course, the subdomain solves have to be of a type that does not rely on a separation of physics.
Some aspects of overlapping domain decomposition and Schwarz methods
In this work, only overlapping domain decompositions (DD) methods are used, while the case of non-overlapping DD methods is not treated at all. In overlapping DD methods, the entire computational domain \(\Omega \) is decomposed into M overlapping subdomains \(\Omega _{m}\) with \(m=1,\ldots ,M\). Then, the problem is reformulated as a local Dirichlet-type problem on each subdomain guaranteeing the well-posedness of all subdomain problems. Exchange of information among the subdomains happens via the overlap of the subdomains. In parallel computer architectures, subdomains \(\Omega _{m}\) are often assigned to processes m to allow for parallel execution and speed-up of the computation.
Two elementary methods, known as additive Schwarz method and multiplicative Schwarz method, will play an important role in defining the FSI preconditioners [32,33,34]. Both are based on an overlapping DD. Starting from a matrix representation that groups unknowns according to subdomains one ends up with an additive Schwarz method by dropping all off-diagonal blocks, which equals a block-Jacobi-like approach. It can be expressed as

Solutions on all subdomains \(\Omega _{m}\) can be computed simultaneously, since they do not depend on the current iterate of other subdomains. In opposite, multiplicative Schwarz methods are obtained by dropping only the upper-triangular off-diagonal blocks, yielding a block-Gauß–Seidel-like approach, which is usually expressed as

Solving for each subdomain needs to be done sequentially since the lower-triangular off-diagonal blocks couple the subdomains and, thus, require the current iterate in subdomain \(m-1\) to be known in order to solve on subdomain m. Following [34], combinations of additive and multiplicative Schwarz methods are often referred to as hybrid Schwarz methods. For further details the reader is referred to literature [32,33,34].
Partitioning and setup of the domain decomposition
A typical overlapping domain decomposition for purely physics-based block preconditioners is illustrated in Fig. 2a.
Overlapping domain decompositions of a FSI problem—Top: At the fluid-structure interface \(\Gamma _\mathrm {FSI}\), the domain is partitioned into solid and fluid subdomains indicated by dashed lines. Each field can further be distributed among several processes by an overlapping domain decomposition indicated by the colored patches. Overlap of subdomains is not depicted for clarity of presentation. Bottom: In a decomposition based on a monolithic graph, subdomains span across the interface like ’proc 0’ and ’proc 2’. They are crucial for the effectiveness of the proposed preconditioner. Some processes might not own portions of both fields, e.g. ’proc 1’. Overlap of subdomains is not depicted for clarity of presentation
The entire computational domain \(\Omega \) is separated into a solid domain  and a fluid domain
and a fluid domain  by the fluid-structure interface \(\Gamma _\mathrm {FSI}\). To speed up computations on parallel hardware architectures, each physical field can be partitioned among \(M\) parallel processes by an overlapping domain decomposition, cf. ’proc 0’, ’proc 1’, and ’proc 2’ in Fig. 2a. For simplicity of illustration, coloring of the subdomains is done based on the ’interior’ nodes of each subdomain, while the overlap is not visualized. There are independent domain decompositions of the solid and the fluid field, where subdomain boundaries at the interface inside the solid domain do not necessarily coincide with subdomain boundaries of the fluid field such that every process handles a portion of each field, i.e. owns nodes of both solid and fluid subdomains. This is not necessarily the case in other implementations but arises naturally in a multi-physics framework that deals with one field after another.Footnote 2
by the fluid-structure interface \(\Gamma _\mathrm {FSI}\). To speed up computations on parallel hardware architectures, each physical field can be partitioned among \(M\) parallel processes by an overlapping domain decomposition, cf. ’proc 0’, ’proc 1’, and ’proc 2’ in Fig. 2a. For simplicity of illustration, coloring of the subdomains is done based on the ’interior’ nodes of each subdomain, while the overlap is not visualized. There are independent domain decompositions of the solid and the fluid field, where subdomain boundaries at the interface inside the solid domain do not necessarily coincide with subdomain boundaries of the fluid field such that every process handles a portion of each field, i.e. owns nodes of both solid and fluid subdomains. This is not necessarily the case in other implementations but arises naturally in a multi-physics framework that deals with one field after another.Footnote 2
We overcome the mismatch of subdomains at the interface by basing the partitioning on a monolithic graph, that consists of the solid and fluid graphs and also reflects the interface coupling. It is created as the combination of the solid and the fluid graph with additional insertion of off-diagonal coupling entries for the interface coupling. In our particular formulation, the coupling can be extracted from the mortar projection operator where a non-zero entry in row \(i\) and column \(j\) indicates the coupling between the \(i\mathrm {th}\) degree of freedom of the slave field to the \(j\mathrm {th}\) degree of freedom of the master field and vice versa.Footnote 3 Then, a topological graph-based partitioner will produce subdomains that are likely to span across the interface as illustrated in Fig. 2b. Interface-spanning subdomains can be fostered further by using a weighted graph with higher weights across and in the vicinity of the interface. At the interface, neighboring solid and fluid subdomains now reside on the same process, namely ’proc 0’ and ’proc 2’ in Fig. 2b. These processes, that ’own’ patches spanning across the interface, will play a key role in the design of the proposed preconditioner. On the other hand, some processes might not own a portion of each field, for example ’proc 1’ in Fig. 2b, that only owns solid nodes, but no fluid and ALE nodes. Again, coloring of the subdomains is done based on the ’interior’ nodes of each subdomain, while the overlap is not visualized for simplicity of illustration.
We rewrite the linear system (1) as
with \(\mathbf {A}\), \(\mathbf {x}\) and \(\mathbf {b}\) replacing the system matrix  , the solution increment vector \(\Delta {\mathbf {x}}\), and the right-hand side vector \(-\mathbf {r}\). This indicates that the actual block structure is of no importance. Sorting all unknowns by their affiliation to parallel subdomains (rather than according to physical fields) yields the matrix representation
, the solution increment vector \(\Delta {\mathbf {x}}\), and the right-hand side vector \(-\mathbf {r}\). This indicates that the actual block structure is of no importance. Sorting all unknowns by their affiliation to parallel subdomains (rather than according to physical fields) yields the matrix representation
distributed among n subdomains, where n usually equals the number of processes \(n^{proc}\). Matrices \(\mathbf {A}_{ii}\) are restrictions of the global matrix \(\mathbf {A}\) to process i, while off-diagonal matrices \(\mathbf {A}_{ij}\) and \(\mathbf {A}_{ji}\) account for the coupling between neighboring subdomains on processes i and j. For non-neighboring subdomains i and j, it is \(\mathbf {A}_{ij}=\mathbf {0}\) and \(\mathbf {A}_{ji}=\mathbf {0}\). All process-local matrices in (12) are sparse. We stress that this partitioning is not aligned with the FSI interface \(\Gamma _\mathrm {FSI}\).
Setup and application of the preconditioner
To set up the hybrid preconditioner, two building blocks are necessary, namely one of the aforementioned physics-based block preconditioners from “Physics-based block preconditioning tailored to fluid–structure interaction” section (or the reader’s favorite choice) plus the additional interface preconditioner. We denote the physics-based block preconditioner by  , while the additional interface preconditioner is referred to as
, while the additional interface preconditioner is referred to as  .
.
For the construction of  , we define two distinct sets
, we define two distinct sets
where \({\mathcal {S}}_{\gamma }\) contains all subdomains \(\Omega _{i}\) that are intersected by the interface \(\Gamma _\mathrm {FSI}\) and \({\mathcal {S}}_{\iota }\) is the complementary set containing all subdomains that do not own any portion of the interface. Naturally, \({\mathcal {S}}_{\gamma } \cap {\mathcal {S}}_{\iota } = \emptyset \) and \({\mathcal {S}}_{\gamma } \cup {\mathcal {S}}_{\iota }= \Omega \).
We now rearrange the matrix \(\mathbf {A}\) according to the sets \({\mathcal {S}}_{\iota }\) and \({\mathcal {S}}_{\gamma }\) and rearrange entries according to a subdomain-based splitting yielding
The diagonal blocks \(\mathbf {A}_{\iota \iota }\) and \(\mathbf {A}_{\gamma \gamma }\) contain all matrix entries associated with \({\mathcal {S}}_{\iota }\) and \({\mathcal {S}}_{\gamma }\), respectively. The off-diagonal blocks \(\mathbf {A}_{\iota \gamma }\) and \(\mathbf {A}_{\gamma \iota }\) represent the connection of adjacent subdomains in \({\mathcal {S}}_{\iota }\) and \({\mathcal {S}}_{\gamma }\), respectively. A pure interface preconditioner based on additive Schwarz principles now is defined as

It directly addresses error accumulation at the interface since its subdomains are intentionally spanning across the interface. However, it is sub-optimal in terms of parallel efficiency since it only operates on interface-spanning subdomains in \({\mathcal {S}}_{\gamma }\), leaving processes assigned to subdomains in \({\mathcal {S}}_{\iota }\) idle. Without loss of the beneficial smoothing effect across the interface, we rather define the interface preconditioner as

with n being the total number of parallel processes, \(M\). Note that both  and
and  satisfy our initial goal to reduce error accumulation at the fluid-structure interface and, thus, are able to alleviate deficiencies of the non-overlapping DD of physics-based block preconditioners.
satisfy our initial goal to reduce error accumulation at the fluid-structure interface and, thus, are able to alleviate deficiencies of the non-overlapping DD of physics-based block preconditioners.
We employ incomplete LU (ILU) factorizations [35,36,37] to approximate the block inverses in (13) and (14). Note that ILU is insensitive to the mixed solid/fluid nature of the interface-related matrix blocks \(\mathbf {A}_{\gamma \gamma }\). The costs in terms of wall clock time of  do not rise compared to
do not rise compared to  when for example an ILU factorization is computed on all subdomains rather than on the interface-spanning ones only due to the parallel treatment of all subdomains.
when for example an ILU factorization is computed on all subdomains rather than on the interface-spanning ones only due to the parallel treatment of all subdomains.
The physics-based block preconditioner  and the additional interface preconditioner
and the additional interface preconditioner  are chained together to form the hybrid interface preconditioner. Equally, the shorter expression hybrid preconditioner is used in the remainder of this manuscript. It is constructed in a multiplicative Schwarz fashion, reading
are chained together to form the hybrid interface preconditioner. Equally, the shorter expression hybrid preconditioner is used in the remainder of this manuscript. It is constructed in a multiplicative Schwarz fashion, reading

where the additional interface preconditioner  is applied before and after the physics-based block preconditioner
is applied before and after the physics-based block preconditioner  . In GMRES iteration \(k\), the preconditioner (15) is applied to the linear system (11) via three stationary Richardson iterations
. In GMRES iteration \(k\), the preconditioner (15) is applied to the linear system (11) via three stationary Richardson iterations

with damping parameters \(\omega _{\mathrm {\gamma }}\) and \(\omega _{\mathrm {B}}\) and the initial search direction \(\mathbf {s}\) generated by the outer Krylov method. Intermediate steps after the first and second Richardson iteration are denoted by \(\mathbf {z}_{\mathrm {I}}^{k}\) and \(\mathbf {z}_{\mathrm {II}}^{k}\), respectively, while the final result of the preconditioning operation is the preconditioned search direction \(\mathbf {z}_{\mathrm {III}}^{k}\). In principle, it is possible to perform multiple iterations of each of the three Richardson iterations in (16), however this possibility is not exploited here. Additionally, damping parameters are chosen as \(\omega _{\mathrm {\gamma }}=1\) and \(\omega _{\mathrm {B}}=1\) in this work since the step length is determined by the outer Krylov solver.
Remark 2
The hybrid preconditioning method (15) employs the interface preconditioner  twice, namely once before and once after the application of the physics-based block preconditioner
twice, namely once before and once after the application of the physics-based block preconditioner  . One could drop either the pre- or the post-application of
. One could drop either the pre- or the post-application of  , though this approach is not pursued here as it involves the same setup cost but less gain in performance than the original approach (15).
, though this approach is not pursued here as it involves the same setup cost but less gain in performance than the original approach (15).
Remark 3
One-level additive Schwarz methods, e.g. such as  , are known to result in increased iteration counts when the number of subdomains is increased and the element overlap is constant [33]. Thus, the additive Schwarz preconditioner
, are known to result in increased iteration counts when the number of subdomains is increased and the element overlap is constant [33]. Thus, the additive Schwarz preconditioner  is always applied in the hybrid setting together with a physics-based multigrid preconditioner, e.g. as given in (15), to enable mesh independence as will be demonstrated in the numerical example in “Performance analysis” section.
is always applied in the hybrid setting together with a physics-based multigrid preconditioner, e.g. as given in (15), to enable mesh independence as will be demonstrated in the numerical example in “Performance analysis” section.
Remark 4
The physics-based block preconditioner  depends on the ordering of the unknowns, exemplarily evidenced by the forward BGS preconditioner
depends on the ordering of the unknowns, exemplarily evidenced by the forward BGS preconditioner  defined in (2), which relies on the ordering of the unknowns to be
defined in (2), which relies on the ordering of the unknowns to be  . In the context of BGS preconditioners, this ordering matters, and a different ordering affects the solution process. For Schur complement preconditioners, different orderings have been studied by Langer and Yang [15]. However, the additional interface preconditioner
. In the context of BGS preconditioners, this ordering matters, and a different ordering affects the solution process. For Schur complement preconditioners, different orderings have been studied by Langer and Yang [15]. However, the additional interface preconditioner  does not make any assumption about a particular ordering of unknowns. The proposed hybrid preconditioner is constructed such that it can be used not only with
does not make any assumption about a particular ordering of unknowns. The proposed hybrid preconditioner is constructed such that it can be used not only with  type physics-based block preconditioners, but also with physics-based block preconditioners that employ different orderings of unknowns.
type physics-based block preconditioners, but also with physics-based block preconditioners that employ different orderings of unknowns.
Error assessment for the hybrid interface preconditioner
In “Error assessment for physics-based block preconditioners” section, we have introduced the error of the preconditioning operation when using physics-based block preconditioners. We now perform such an analysis for the additional interface preconditioner \(\varvec{\mathscr {M}}_{\mathrm {\gamma }}\). Therefore, we utilize the splitting of all subdomains into the sets \({\mathcal {S}}_{\iota }\) and \({\mathcal {S}}_{\gamma }\).
The error matrix for the interface preconditioner \(\varvec{\mathscr {M}}_{\mathrm {\gamma }}\) from (14) is given as

and the error propagation  accordingly reads
accordingly reads

We stress that the error vanishes in subdomains \(\Omega _{i}\in {\mathcal {S}}_{\gamma }, i=0,\ldots ,M- 1\). Errors only occur at the inter-process subdomain boundaries between subdomains \(\Omega _{i}\in {\mathcal {S}}_{\gamma }\) and \(\Omega _{j}\in {\mathcal {S}}_{\iota }\) with \(i,j=0,\ldots ,M- 1, i\ne j\).
A direct comparison of the error propagation  in (7) for the physics-based block preconditioner with
in (7) for the physics-based block preconditioner with  for the interface preconditioner reveals the complementarity of both preconditioners. In particular,
for the interface preconditioner reveals the complementarity of both preconditioners. In particular,  is solely populated in entries related to the fluid-structure interface \(\Gamma _\mathrm {FSI}\), whereas
is solely populated in entries related to the fluid-structure interface \(\Gamma _\mathrm {FSI}\), whereas  does not exhibit any error propagation in interface-spanning subdomains \(\Omega _{i}\in {\mathcal {S}}_{\gamma }, i=0,\ldots ,M- 1\).
does not exhibit any error propagation in interface-spanning subdomains \(\Omega _{i}\in {\mathcal {S}}_{\gamma }, i=0,\ldots ,M- 1\).
Numerical experiments
We evaluate the performance of the proposed preconditioning technique using two examples. First, the well-known pressure wave example is studied, which is often seen as a benchmark case to assess the performance of FSI solvers. We also assess the hybrid preconditioner using a computational model of a Coriolis flow meter where the fluid flow is highly convective.
To assess the performance impact of the proposed preconditioner, we consider (i) the number of necessary Krylov iterations until convergence, (ii) the wall clock time spent in the solution process excluding setup of the preconditioner, and (iii) timings including the setup of the preconditioner. This allows to evaluate the overall performance impact and to quantify total speed-ups.
Pressure wave through an elastic tube
As a benchmark problem for monolithic FSI solvers, the well-known pressure wave through an elastic tube, originally proposed in [38], is studied. It is designed to mimic hemodynamic conditions, especially w.r.t. to the material densities with the ratio  . Mayr et al. [1] used this example to discuss the influence of different time integration schemes on the solution and also demonstrated correctness of the solution via temporal and spatial convergence studies. A detailed analysis of the performance of the linear solvers has been performed in [6] where classical versions of the FSI-specific AMG preconditioners from “Physics-based block preconditioning tailored to fluid–structure interaction” section have been applied. Simulations with non-matching interface discretizations have been reported in literature, either employing a dual mortar method [30] or radial basis function inter-grid transfer operators [39,40,41]. It is often used as a benchmark for partitioned [42,43,44,45,46,47] and monolithic solvers [2, 8, 15, 22, 23, 48] among others.
. Mayr et al. [1] used this example to discuss the influence of different time integration schemes on the solution and also demonstrated correctness of the solution via temporal and spatial convergence studies. A detailed analysis of the performance of the linear solvers has been performed in [6] where classical versions of the FSI-specific AMG preconditioners from “Physics-based block preconditioning tailored to fluid–structure interaction” section have been applied. Simulations with non-matching interface discretizations have been reported in literature, either employing a dual mortar method [30] or radial basis function inter-grid transfer operators [39,40,41]. It is often used as a benchmark for partitioned [42,43,44,45,46,47] and monolithic solvers [2, 8, 15, 22, 23, 48] among others.
The geometry is depicted in Fig. 3. The solid tube is clamped at both ends. The fluid is initially at rest. For the duration of \({3\cdot 10^{-3}}\,{\hbox {s}}\), it is loaded with a surface traction  in \(z\)-direction at \(z=0\). At \(z=\ell \), fluid velocities are prescribed to zero, meaning that the tube is closed at that end. As a result, a pressure wave travels along the tube’s longitudinal axis and is reflected at the closed end of the tube. The constitutive behavior of the structure is modelled by a St.-Venant-Kirchhoff material with Young’s modulus
in \(z\)-direction at \(z=0\). At \(z=\ell \), fluid velocities are prescribed to zero, meaning that the tube is closed at that end. As a result, a pressure wave travels along the tube’s longitudinal axis and is reflected at the closed end of the tube. The constitutive behavior of the structure is modelled by a St.-Venant-Kirchhoff material with Young’s modulus  , Poisson’s ratio
, Poisson’s ratio  , and density
, and density  . The fluid is assumed to be an incompressible Newtonian fluid with dynamic viscosity
. The fluid is assumed to be an incompressible Newtonian fluid with dynamic viscosity  and density
and density  .
.
Here, the solid is discretized with Hex8 F-bar elements [49], while the fluid utilizes P1P1 elements with residual-based stabilization as briefly outlined in “The monolithic solution method for FSI” section. Different meshes are studied as detailed in Table 1. Mesh independency has been studied in our previous work [1]. Based on these results, all meshes used in this study are considered as fine enough to render mesh independency of the solution. Simulations have been performed on an Opteron based cluster.Footnote 4 The load per parallel process is kept approximately constant at \(\approx 7620\,n^\mathrm {dof}/\mathrm {process}\).
Figure 4a shows a snapshot of the solution at time \(t={0.005}\,{\sec }\). Diagrams of the solid’s radial displacement as well as the fluid pressure at half length of the pipe \((z={2.5}\, {\hbox {cm}})\) can be found in Fig. 4b.
The subsequent analysis of the proposed preconditioners is divided into two parts. First, “Proof of concept and demonstration of improved error reduction” section considers a small problem size and studies the linear solution process in detail as a demonstrator of the new hybrid interface preconditioner. A comparison to the physics-based block preconditioners including a quantification of the preconditioning effect is carried out. Second, a performance analysis of the new hybrid preconditioner applied to all meshes pw1–pw6 is presented in “Performance analysis” section.
Proof of concept and demonstration of improved error reduction
To demonstrate the basic principle behind the proposed hybrid preconditioner numerically, a reduced-size version of the pressure wave example is studied. A coarse mesh is used. The solid portion consists of 5904 unknowns, while fluid and ALE use 15908 and 11, 931 degrees of freedom, respectively. The total number of unknowns is 33, 743. The problem is solved on 4 processes using an overlapping domain decomposition based on a monolithic graph of the coupled problem.
For simplicity, only the linear system of equations in the first nonlinear iteration of the first time step is considered. This system can be seen as exemplary for all time steps of the simulation, since linear and nonlinear iteration counts are rather constant throughout the entire simulation as will be seen in “Performance analysis” section. The effectiveness of the hybrid preconditioner is assessed by comparing error reduction through different preconditioners. On the one hand, the purely physics-based block-iterative preconditioner summarized in “A block-iterative approach with internal algebraic multigrid preconditioners” section is used. Applying exact block inverses with LU decompositions for each block within the BGS method, errors after application of the preconditioner are only due to the outer BGS method. This preconditioner is referred to as BGS(LU). On the other hand, the proposed hybrid preconditioner is configured as follows: The interface part  of the preconditioner uses direct LU-based solves for each subdomain, while the physics-based block preconditioning part
of the preconditioner uses direct LU-based solves for each subdomain, while the physics-based block preconditioning part  is the aforementioned BGS(LU) approach to augment comparability. It is referred to as H-BGS(LU).
is the aforementioned BGS(LU) approach to augment comparability. It is referred to as H-BGS(LU).
Two tests are performed: First, effectiveness of the hybrid preconditioner is assessed in terms of the number of GMRES iterations required to reach machine precision, i.e. \(\left\| \mathbf {r}_{\mathrm {lin}}^{i}\right\| _{2}/\left\| \mathbf {r}_{\mathrm {lin}}^{0}\right\| _{2} < 10^{-15}\). The pure BGS(LU) preconditioned method requires 41 GMRES iterations and therefore 41 applications of BGS(LU). The hybrid H-BGS(LU) requires 11 GMRES iterations, where each iteration consists of one BGS(LU) and two applications of  , cf. (15). This totals 33 single-stage preconditioner applications compared to the 41 applications for the pure BGS(LU).
, cf. (15). This totals 33 single-stage preconditioner applications compared to the 41 applications for the pure BGS(LU).
Second, the number of GMRES iterations is limited as follows. The effect of preconditioning is evaluated by the achieved relative residual reduction as well as the remaining error, i.e. the deviation of the approximate GMRES solution from the pre-computed exact solution. For H-BGS(LU), a single GMRES iteration is performed. One sweep of H-BGS(LU) consists of three applications of LU-type preconditioners, namely the pre- and post-application of  plus one sweep of BGS(LU) in between. To achieve comparability, three GMRES iterations are performed with pure BGS(LU) to also apply a LU-type method three times in total. The results are summarized in Table 2. One iteration with H-BGS(LU) achieves a relative residual reduction \(\left\| \mathbf {r}_{\mathrm {lin}}^{1}\right\| _{2}/\left\| \mathbf {r}_{\mathrm {lin}}^{0}\right\| _{2}=6.9\cdot 10^{-3}\), while three iterations with BGS(LU) yield a reduction of only \(\left\| \mathbf {r}_{\mathrm {lin}}^{3}\right\| _{2}/\left\| \mathbf {r}_{\mathrm {lin}}^{0}\right\| _{2}=5.2\cdot 10^{-2}\).
plus one sweep of BGS(LU) in between. To achieve comparability, three GMRES iterations are performed with pure BGS(LU) to also apply a LU-type method three times in total. The results are summarized in Table 2. One iteration with H-BGS(LU) achieves a relative residual reduction \(\left\| \mathbf {r}_{\mathrm {lin}}^{1}\right\| _{2}/\left\| \mathbf {r}_{\mathrm {lin}}^{0}\right\| _{2}=6.9\cdot 10^{-3}\), while three iterations with BGS(LU) yield a reduction of only \(\left\| \mathbf {r}_{\mathrm {lin}}^{3}\right\| _{2}/\left\| \mathbf {r}_{\mathrm {lin}}^{0}\right\| _{2}=5.2\cdot 10^{-2}\).
A visualization of the distribution of the error over a cross section of the domain is shown in Fig. 5 to demonstrate error accumulation at the fluid-structure interface. For the pure BGS(LU) preconditioner, the error after three GMRES iterations is plotted in Fig. 5a. In the solid, the error is at the order of \(10^{-4}\) (left) with slightly larger values at the fluid-structure interface. The accumulation of error at the interface is even more pronounced for the fluid velocity (middle) and fluid pressure (right), which are of order \(10^{0}\) and \(10^{4}\), respectively. The same analysis for the hybrid preconditioner H-BGS(LU) is shown in Fig. 5b, showing that significantly better error reductions could be achieved. In particular, the effect of the interface preconditioner becomes evident in the fluid field where the larger errors in fluid velocities and fluid pressure are now located in the center of the domain as opposed to the pure BGS(LU) preconditioning where higher errors occurred at the FSI interface. The maximum error in solid displacements is at the order of \(10^{-8}\), which resembles a reduction by four orders of magnitude. Similar reductions are achieved for errors in fluid velocities and fluid pressure, where maximum values are now at the order of \(10^{-4}\) and \(10^{-1}\), respectively. A graphical comparison is given in Fig. 5c. Therein, the circular geometry is cut in half. The upper half reports the errors for pure BGS(LU), the lower half those for H-BGS(LU). Color scales are calibrated such that they span the combined range of errors of BGS(LU) and H-BGS(LU). The reductions of the error by the hybrid preconditioner compared to the purely physics-based one can be seen clearly. Summarizing, the idea behind the hybrid interface preconditioner could be confirmed numerically.
Performance analysis
To study the hybrid preconditioner on a larger scale, the hybrid strategy is applied to the existing physics-based block preconditioners from “Physics-based block preconditioning tailored to fluid–structure interaction” section. The pressure wave problem is solved on the series of meshes detailed in Table 1 to study the influence of mesh refinement and an increased number of parallel processes. Thereby, the load per parallel process is kept approximately constant, rendering a weak scaling type of study.Footnote 5 The numbers of parallel processes are chosen such that the average load per process is roughly \(7620\,n^\mathrm {dof}/\mathrm {process}\) for each mesh, such that local subdomains are of a size that is reasonably treated with incomplete LU or LU factorizations.
A prerequisite for the application of the hybrid preconditioner is the overlapping domain decomposition with subdomains that span across the fluid-structure interface, cf. “Partitioning and setup of the domain decomposition” section. A comparison of the domain decompositions for physics-based and hybrid preconditioners for a total number of parallel processes of \(M=32\) is shown in Fig. 6. Starting from an initial, field-wise partitioning as shown in Fig. 6a, a monolithic graph containing solid and fluid graphs is built. This is passed to the hyper-graph partitioner package Zoltan [50] to obtain a parallel layout as it is required for the hybrid preconditioner. The final monolithic partitioning exhibits subdomains that span across the fluid-structure interface as desired, cf. Fig. 6b.
The cut view illustrates the parallel distribution of the entire problem among 32 processes. Black lines indicate the interface position. Left: When solid and fluid domain have been distributed independently, subdomains do not span across the interface. Right: After redistribution based on a monolithic graph, some subdomains contain solid or fluid portions only, while a certain number of subdomains contains solid and fluid portions and span across the interface
In this study, the following preconditioner configurations are examined: The one-level additive Schwarz part of the hybrid preconditioner applies an ILU(0) locally on each subdomain. It is applied before and after the physics-based multi-level block preconditioner. We study both variants, namely BGS(AMG) and AMG(BGS), for the physics-based block preconditioner with the configurations summarized in Table 3. Each preconditioner is created once at the beginning of each time step and is then re-used in every nonlinear iteration of that time step. The convergence check is performed as detailed in Appendix A. For the nonlinear solver, absolute norms of residual vectors and solution vector increments are required to be smaller than \(10^{-6}\) for solid and fluid field, while a tolerance of \(10^{-7}\) is demanded at the interface. The linear solver uses the relative tolerance \(\varepsilon ^\mathrm {lin}=10^{-5}\) in combination with \(\beta ^\mathrm {lin}=10^{-3}\).
Iteration counts and timings for hybrid preconditioners applied to mesh pw6 of pressure wave example on 256 parallel processes—iterations, setup and iteration timings are almost constant over all time steps. Application of the hybrid preconditioner leads to a reduction of iterations and solver time for every type of underlying physics-based block preconditioner. The additional setup cost for the hybrid preconditioner is amortized
Iteration counts, pure linear solver time, and total linear solver time including setup are reported in Fig. 7 for the finest mesh pw6. Solid lines represent the hybrid preconditioner denoted by the prefix ’H-’, while dashed lines indicate the classic, purely physics-based block preconditioners for the sake of comparison. The additional additive Schwarz preconditioner enhances the preconditioner such that the number of linear iterations is reduced in every configuration, cf. Fig. 7a. A very similar picture can be seen w.r.t. the timings of the linear solver. In Fig. 7b, the reduced number of iterations in case of the hybrid preconditioner results in a reduction of the pure solver time, i.e. when excluding the setup time of the preconditioner. These savings can also be seen in the total timings of the linear solver that also include the setup cost of the preconditioner, cf. Fig. 7c. Since the setup cost of the hybrid preconditioner are larger than those of the pure physics-based block preconditioners, the relative savings are lower than in the pure solver time, but still amortize the additional setup costs. Respective diagrams for the coarser meshes pw1–pw5 are omitted for brevity of presentation, but are summarized in Table 4. A comparison among all meshes allows for studying the influence of the mesh size and of the number of parallel processes. Considering the number of GMRES iterations, they remain almost constant under mesh refinement for all preconditioning approaches despite an increased number of subdomains and a decreased overlap as it is expected for multigrid approaches. Timings of the linear solver exhibit slight increases when refining the mesh. When increasing the problem size by a factor of 16, the timings increase by a factor of 5. There are several reasons for these increases: Due to the fully coupled AMG preconditioner, internal coarse-level load rebalancing in the ML [51] package cannot be applied which is crucial for scalability. This leads to a coarse level systems that are far too small to be solved efficiently on a large number of parallel processes and whose solution requires much communication among all processes. Hardware limitations and communication patterns surely contribute to increased timings as well.
To assess its efficiency, iteration counts and solver timings with and without the hybrid preconditioner have been accumulated over each time step and are compared in Table 4, where also relative savings of iterations and solver time are reported. These savings amortize the additional effort during setup. The extra setup cost is governed by the size of the subdomains, since the ILU factorization on each parallel process can be performed in parallel independently of each other. If the load per process is kept constant, the additional setup cost is independent of the problem size or the number of processes, respectively.
Remark 5
For the process-local subdomain solves involved in the  part of the hybrid preconditioner, larger fill levels than ILU(0) have been investigated. In this case, the huge increase in setup cost cannot be amortized by the improved quality of the preconditioner. If the local subdomains are sufficiently small, an exact direct solve seems to be a viable choice, however it is outperformed by the ILU(0) option. Summing up, ILU(0) seems to be a good trade-off between setup cost and effectiveness of the preconditioner.
part of the hybrid preconditioner, larger fill levels than ILU(0) have been investigated. In this case, the huge increase in setup cost cannot be amortized by the improved quality of the preconditioner. If the local subdomains are sufficiently small, an exact direct solve seems to be a viable choice, however it is outperformed by the ILU(0) option. Summing up, ILU(0) seems to be a good trade-off between setup cost and effectiveness of the preconditioner.
Coriolis flow meter
To also study the performance in case of convection-dominated flow fields, a Coriolis flow meter is simulated where our model is inspired by the presentation in [52]. Such devices measure the fluid mass flow rate directly. The setup is as follows: The fluid flow is directed through a bent pipe while the pipe is forced into an oscillatory motion in its first bending mode, i.e. the bending of the pipe around the y-axis, cf. Fig. 8a. Due to the Coriolis effect, the pipe exhibits a twisting deformation where the amplitude of twisting angle depends on the fluid mass flow rate. By measuring the amplitude of the twisting angle, highly accurate measurements of the fluid mass flow rate can be provided. Since the enclosed fluid mass has to follow the bending and twisting motion of the solid pipe, this example challenges the FSI solution algorithm due to the ALE-based fluid description.
Coriolis flow meter—Top: The U-shaped pipe with circular cross section is clamped at its inflow and outflow cross sections and filled with fluid. The fluid velocity is prescribed at the inflow, while a traction-free boundary condition is assumed at the outflow. Bottom left: Snapshot of solution with displacement of the pipe and velocity profiles of the fluid flow. Bottom right: Vertical displacement over time
The domain including geometric dimensions and boundary conditions is depicted in Fig. 8a. The solid pipe is modelled with a compressible Neo–Hookean material [53] with Young’s modulus  , Poisson’s ratio
, Poisson’s ratio  and density
and density  , while the incompressible fluid is assumed to be Newtonian with dynamic viscosity
, while the incompressible fluid is assumed to be Newtonian with dynamic viscosity  and density
and density  . The pipe is clamped at the inflow and outflow cross sections. Starting from resting initial conditions, the inflow velocity is prescribed as a spatially parabolic inflow profile with the time-dependent peak value
. The pipe is clamped at the inflow and outflow cross sections. Starting from resting initial conditions, the inflow velocity is prescribed as a spatially parabolic inflow profile with the time-dependent peak value

with  and \(t_1={1.8}\,{\hbox {s}}\). The periodic external excitation force is oriented in \(z\)-direction and is given as
and \(t_1={1.8}\,{\hbox {s}}\). The periodic external excitation force is oriented in \(z\)-direction and is given as

with the amplitude  , the angular frequency
, the angular frequency  and \(t_2={2.0}\,{\hbox {s}}\). It acts on the outer surface of the pipe in the gray-shaded area in Fig. 8a. The twisting angle amplitude that is needed for the mass flow measurement can be derived from the displacements in z-direction in locations A and B. A snapshot of the solution is depicted in Fig. 8b and the evolution of the vertical displacement of the characteristic point C defined in the problem sketch is shown in Fig. 8c.
and \(t_2={2.0}\,{\hbox {s}}\). It acts on the outer surface of the pipe in the gray-shaded area in Fig. 8a. The twisting angle amplitude that is needed for the mass flow measurement can be derived from the displacements in z-direction in locations A and B. A snapshot of the solution is depicted in Fig. 8b and the evolution of the vertical displacement of the characteristic point C defined in the problem sketch is shown in Fig. 8c.
For the numerical simulation, units for length, time, and mass are chosen as \({\hbox {mm}}\) (millimeter), \({\hbox {s}}\) (second), and \({\hbox {g}}\) (gram), respectively. The solid is discretized with Hex8 F-bar elements [49], while the fluid utilizes Hex8 P1P1 elements with residual-based stabilization. Different meshes with matching grids at the interface are studied as detailed in Table 5. Time integration is performed by the generalized-\(\alpha \) method for solid dynamics [54] and fluid dynamics [55] with spectral radii  and
and  , respectively. The time step size is chosen as \(\Delta {t}={0.005}\,{\hbox {s}}\) for the results presented below. The solid field is selected as master field, i.e. the interface motion is described in terms of solid displacements.
, respectively. The time step size is chosen as \(\Delta {t}={0.005}\,{\hbox {s}}\) for the results presented below. The solid field is selected as master field, i.e. the interface motion is described in terms of solid displacements.
Simulations have been performed on the Haswell Xeon partitionFootnote 6 of the SuperMUC Petascale System at the Leibniz Supercomputing Centre in Garching, Germany. The load per parallel process is kept approximately constant at an average of \(\approx 15565\,n^\mathrm {dof}/\mathrm {process}\).
The configuration of the multigrid preconditioners is summarized in Table 6. Each preconditioner is created once at the beginning of each time step and is then re-used in every nonlinear iteration of that time step. To account for different transient effects in the solid and the fluid field as well as for the chosen set of physical units, the convergence check is performed as outlined in Appendix A. Tolerances for the convergence check of the nonlinear solver are listed in Table 7. The linear solver uses the relative tolerance \(\varepsilon ^\mathrm {lin}=10^{-5}\) in combination with \(\beta ^\mathrm {lin}=10^{-2}\).
A comparison of iteration counts, solver timings and preconditioner setup timings for all preconditioners and meshes is shown in Table 8. Again, savings in linear iterations as well as pure solver time have been achieved by augmenting either of the physics-based block preconditioner with the hybrid approach (see columns labelled with “\(\#\) of linear iterations” and “Solver time” in Table 8). The savings are particularly noticeable in the case of H-AMG(BGS) where the AMG(BGS) part can very much benefit from the smooth interface solution yielded by the pre-application of the interface preconditioner  . In the presence of a convective flow, the gain in efficiency seems to be more pronounced for larger problem sizes, where reductions of the linear solver time of up to \(\approx 43\%\) can be achieved by the hybrid preconditioner. However, we observe that even though AMG(BGS) performs better as compared to BGS(AMG) with respect to the number of GMRES iterations, its pure solver time is not comparable due to the missing coarse level load rebalancing within the AMG(BGS) multi-level hierarchy. Still, the savings due to the hybrid preconditioner H-AMG(BGS) can be seen clearly when comparing to the purely physics-based AMG(BGS) approach. As expected, setup times for the hybrid preconditioner are slightly higher than for the pure physics-based preconditioners due to the additional setup costs for
. In the presence of a convective flow, the gain in efficiency seems to be more pronounced for larger problem sizes, where reductions of the linear solver time of up to \(\approx 43\%\) can be achieved by the hybrid preconditioner. However, we observe that even though AMG(BGS) performs better as compared to BGS(AMG) with respect to the number of GMRES iterations, its pure solver time is not comparable due to the missing coarse level load rebalancing within the AMG(BGS) multi-level hierarchy. Still, the savings due to the hybrid preconditioner H-AMG(BGS) can be seen clearly when comparing to the purely physics-based AMG(BGS) approach. As expected, setup times for the hybrid preconditioner are slightly higher than for the pure physics-based preconditioners due to the additional setup costs for  , but overall are independent of the mesh size (see column labelled with “Setup time” in Table 8). Savings are not given for setup times, since setup time is expected to increase. Only for mesh cor1, the overall time-to-solution, i.e. combined setup and solver time, is not greatly affected by the hybrid preconditioner, whereas it is reduced for the finer meshes cor2 and cor3. Overall, the additional setup time for
, but overall are independent of the mesh size (see column labelled with “Setup time” in Table 8). Savings are not given for setup times, since setup time is expected to increase. Only for mesh cor1, the overall time-to-solution, i.e. combined setup and solver time, is not greatly affected by the hybrid preconditioner, whereas it is reduced for the finer meshes cor2 and cor3. Overall, the additional setup time for  is amortized by the achieved performance gain.
is amortized by the achieved performance gain.
Oscillating flexible flag behind a rigid obstacle
To showcase the behavior of the proposed preconditioner in the presence of large mesh deformation, we study the oscillating bending motion of a flexible solid flag attached to a rigid obstacle and subject to fluid flow as first proposed by Wall [56]. The flexible flag  is modelled with a Neo-Hooke material (Young’s modulus
is modelled with a Neo-Hooke material (Young’s modulus  ,
,  ,
,  ) and is attached to a rigid obstacle as depicted in Fig. 9. Both are immersed in the fluid domain
) and is attached to a rigid obstacle as depicted in Fig. 9. Both are immersed in the fluid domain  (
( ,
,  ). Starting from resting initial conditions, the inflow velocity is prescribed as a spatially constant inflow profile with the time-dependent peak value
). Starting from resting initial conditions, the inflow velocity is prescribed as a spatially constant inflow profile with the time-dependent peak value

with peak value  . The outflow at \(x=14\) serves as a traction-free Neumann boundary. Top and bottom walls have a slip boundary condition. The ALE mesh can slide along inflow, outflow, top and bottom edges and is fixed in the channel’s corners as well as along the obstacle’s edges. Due to large deformations, the ALE mesh is treated as a nonlinear quasi-static solid body with Neo-Hooke material. In particular, the ALE mesh is divided into a stiff, medium, and soft zone with Young’s moduli
. The outflow at \(x=14\) serves as a traction-free Neumann boundary. Top and bottom walls have a slip boundary condition. The ALE mesh can slide along inflow, outflow, top and bottom edges and is fixed in the channel’s corners as well as along the obstacle’s edges. Due to large deformations, the ALE mesh is treated as a nonlinear quasi-static solid body with Neo-Hooke material. In particular, the ALE mesh is divided into a stiff, medium, and soft zone with Young’s moduli  ,
,  , and
, and  and Poisson’s ratios
and Poisson’s ratios  ,
,  , and
, and  , respectively. An exemplary coarse version of the ALE mesh indicating the stiff, medium, and soft region is depicted in Fig. 10 along with a diagram of the vertical tip displacement
, respectively. An exemplary coarse version of the ALE mesh indicating the stiff, medium, and soft region is depicted in Fig. 10 along with a diagram of the vertical tip displacement  and a contour plot of the fluid velocity field on the deformed mesh at maximum deflection of the flag.
and a contour plot of the fluid velocity field on the deformed mesh at maximum deflection of the flag.
Top left: Mesh with stiff, medium, and soft ALE regions colored in blue, red, and black, respectively. Top right: Tip displacement of the flexible flag over time: the amplitude is larger than half the flag length, indicating large deformations. Bottom: Fluid velocity field and deformed mesh at state of maximum deflection at time \(t=4.39\)
The solid is discretized with four-noded linear Wall elements using enhanced assumed strains (EAS), while the fluid field utilizes equal-order interpolated stabilized finite elements. The solid and fluid field use generalized-\(\alpha \) time integration with a constant time step size \(\Delta {t}=0.01\) and spectral radii  and
and  , respectively.
, respectively.
The problem size is rather small ( ,
,  ,
,  , \(n^\mathrm {dof}_\mathrm {total}=39702\)), which is mainly due to the two-dimensional problem setup. As a consequence, the solid discretization is too small for a multigrid method, leaving BGS(AMG) with multigrid for fluid and ALE, but a direct solver for the solid block inverse as a viable approach. The configuration of the multigrid preconditioners for fluid and ALE are the same as in the previous example, cf. Table 6. The solid block is sufficiently small to be immediately addressed with a direct solver. The preconditioner is re-computed in every nonlinear iteration. The problem is run on four MPI ranks, yielding \(n^\mathrm {dof}/\mathrm {process}\approx 9925\) as an approximate load per process. To account for different transient effects in the solid and the fluid field as well as for the chosen set of units, the convergence check is performed as outlined in Appendix A. Tolerances for the convergence check of the nonlinear solver are listed in Table 9. The linear solver uses the relative tolerance \(\varepsilon ^\mathrm {lin}=10^{-5}\) in combination with \(\beta ^\mathrm {lin}=10^{-3}\).
, \(n^\mathrm {dof}_\mathrm {total}=39702\)), which is mainly due to the two-dimensional problem setup. As a consequence, the solid discretization is too small for a multigrid method, leaving BGS(AMG) with multigrid for fluid and ALE, but a direct solver for the solid block inverse as a viable approach. The configuration of the multigrid preconditioners for fluid and ALE are the same as in the previous example, cf. Table 6. The solid block is sufficiently small to be immediately addressed with a direct solver. The preconditioner is re-computed in every nonlinear iteration. The problem is run on four MPI ranks, yielding \(n^\mathrm {dof}/\mathrm {process}\approx 9925\) as an approximate load per process. To account for different transient effects in the solid and the fluid field as well as for the chosen set of units, the convergence check is performed as outlined in Appendix A. Tolerances for the convergence check of the nonlinear solver are listed in Table 9. The linear solver uses the relative tolerance \(\varepsilon ^\mathrm {lin}=10^{-5}\) in combination with \(\beta ^\mathrm {lin}=10^{-3}\).
Figure 11 compares the number of iterations per time step for the BGS(AMG) and H-BGS(AMG) preconditioner. Again, the hybrid preconditioner leads to a reduction of GMRES iterations per time step (by 36% on average) and is therefore equally well applicable to problems with large mesh deformation or distortion.
Concluding remarks and outlook
Starting from existing physics-based AMG block preconditioners for FSI problems, their error accumulation at the fluid-structure interface has been analyzed. To address this drawback, we have developed a hybrid interface preconditioner. It combines the multigrid performance of existing physics-based block preconditioners with an additional additive Schwarz preconditioner that is specifically designed to tackle error accumulation at the fluid-structure interface. This was achieved by generating an overlapping domain decomposition with subdomains that intentionally span across the interface. Incomplete LU factorizations have been found to be a viable choice as subdomain solvers. They seem to represent a good trade-off between setup cost and quality of the result.
A thorough study of the presented preconditioning techniques has been performed. Therein, we examined the well-known pressure wave example, the flow through a Coriolis flow meter, as well as an oscillating flexible flag subject to fluid flow. The influence of the problem size has been investigated. Performance was assessed in terms of numbers of GMRES iterations as well as in terms of solver timings also including setup of the preconditioner. Optimal performance of the physics-based block preconditioners could be reproduced. Furthermore, the application of the hybrid interface preconditioner resulted in reductions of the number of linear iterations as well as the total time spent in the linear solver. These savings have been shown to be independent of the mesh size and the number of processors used for the computation as well as the convection in the flow field. Overall, the performance of existing FSI preconditioners could be enhanced by the hybrid augmentation yielding a preconditioner where the additional effort in the preconditioner setup is fully paid off by the gain of efficiency.
We believe that the underlying idea of the presented preconditioning approach is appealing also for a variety of other applications. Besides FSI problems, it could be applied to any other surface-coupled multi-physics problem like the transport of a scalar species through a FSI interface [57] or a membrane [58, 59], the heat transfer through surfaces of objects, or the interaction of an acoustic field with either a solid or a fluid domain. Moreover, the presence of anisotropic meshes as in fluid boundary layer meshes often spoils the optimality of existing multigrid preconditioners. Applying the hybrid approach in FSI scenarios with such meshes is beneficial. The hybrid preconditioner reduces error accumulation at the interface as intended. In addition, it helps convergence in a boundary layer, where meshes often are anisotropic and the solution exhibits steep gradients. Furthermore, we suppose that the proposed method can be straightforwardly transferred to volume-coupled problems. Strong physics-based block preconditioners are available for such problems, though we suspect that they also exhibit error accumulation in the treatment of the off-diagonal coupling terms between the individual physical fields. This could be cured through the augmentation with an additional additive Schwarz preconditioner as given in (15). Future work will analyze the performance of the proposed method when applied to volume-coupled problems possibly ranging from thermo-elasticity or (ferro-)magnetic elasticity over magneto-hydrodynamics to piezo-mechanics and other multi-physics problems.
In summary, the proposed preconditioning method is attractive for several reasons: It elegantly combines existing preconditioning techniques with an additional preconditioner that specifically addresses the drawbacks of the existing preconditioner. It is applicable to the entire range of surface-coupled multi-physics problems. Last, numerical examples demonstrated its ability to even further enhance the performance of problem-specific preconditioners that already have been shown to be strong.
Notes
Alternative layouts may exist which of course depend on software design. We focus on a modular object-oriented design that handles each physical field inside a multi-physics framework as an independent entity.
AMD Opteron 6128 Magny Cours, nominal frequency of \({2.0}\,{\hbox {GHz}}\), 2 octocore CPUs per node, \({32}\,{\hbox {GB}}\) of memory per node, Infiniband network Mellanox ConnectX with \({40}\,{\hbox {GBit}/\hbox {s}}\).
To the best of our knowledge, there’s no theoretical proof, that multigrid preconditioners for FSI problems can be expected to exhibit \({\mathcal {O}}\left( n\right) \) scalability. In practice, this has also been observed in numerical experiments by others, e.g. in [23].
Haswell Xeon Processor E5-2697 v3 cores, nominal frequency \({2.6}\,{\hbox {GHz}}\), memory per core \({2.3}\,{\hbox {GB}}\), Infiniband FDR14 network; https://www.lrz.de/services/compute/supermuc/systemdescription/, visited on Feb 6, 2017.
References
Mayr M, Klöppel T, Wall WA, Gee MW. A temporal consistent monolithic approach to fluid–structure interaction enabling single field predictors. SIAM J Sci Comput. 2015;37(1):30–59. https://doi.org/10.1137/140953253.
Badia S, Quaini A, Quarteroni A. Modular vs. non-modular preconditioners for fluid-structure systems with large added-mass effect. Comput Methods Appl Mech Eng. 2008;197(49—-50):4216–32.
Causin P, Gerbeau JF, Nobile F. Added-mass effect in the design of partitioned algorithms for fluid-structure problems. Comput Methods Appl Mech Eng. 2005;194(42–44):4506–27.
Heil M, Hazel A, Boyle J. Solvers for large-displacement fluid-structure interaction problems: segregated versus monolithic approaches. Comput Mech. 2008;43(1):91–101.
Küttler U, Gee MW, Förster C, Comerford A, Wall WA. Coupling strategies for biomedical fluid-structure interaction problems. Int J Numer Methods Biomed Eng. 2010;26(3–4):305–21. https://doi.org/10.1002/cnm.1281.
Gee MW, Küttler U, Wall WA. Truly monolithic algebraic multigrid for fluid-structure interaction. Int J Numer Methods Eng. 2011;85(8):987–1016. https://doi.org/10.1002/nme.3001.
Heil M. An efficient solver for the fully coupled solution of large-displacement fluid-structure interaction problems. Comput Methods Appl Mech Eng. 2004;193(1–2):1–23.
Küttler U. Effiziente Lösungsverfahren für Fluid-Struktur-Interaktions-Probleme. München: Dissertation, Technische Universität München; 2009.
Langer U, Yang H. 5. Recent development of robust monolithic fluid-structure interaction solvers. Radon Series on Computational and Applied Mathematics, vol. 20. Berlin: De Gruyter; 2017. p. 169–91.
Richter T. A monolithic geometric multigrid solver for fluid–structure interactions in ALE formulation. Int J Numer Methods Eng. 2015;104(5):372–90.
Tezduyar TE, Sathe S. Modelling of fluid–structure interactions with the space-time finite elements: solution techniques. Int J Numer Methods Fluids. 2007;54(6–8):855–900. https://doi.org/10.1002/fld.1430.
Saad Y, Schultz MH. GMRES: a generalized minimal residual algorithm for solving non-symmetric linear systems. SIAM J Sci Stat Comput. 1986;7(3):856–69.
Sala MG, Tuminaro RS. A new Petrov-Galerkin smoothed aggregation preconditioner for non-symmetric linear systems. SIAM J Sci Comput. 2008;31(1):143–66. https://doi.org/10.1137/060659545.
Vaněk P, Mandel J, Brezina M. Algebraic multigrid by smoothed aggregation for second and fourth order elliptic problems. Computing. 1996;56:179–96.
Langer U, Yang H. Robust and efficient monolithic fluid–structure-interaction solvers. Int J Numer Methods Eng. 2016;108(4):303–25. https://doi.org/10.1002/nme.5214.
Jodlbauer D, Langer U, Wick T. Parallel block-preconditioned monolithic solvers for fluid–structure interaction problems. Int J Numer Methods Eng. 2019;117(6):623–43. https://doi.org/10.1002/nme.5970.
Verdugo F, Wall WA. Unified computational framework for the efficient solution of \(n\)-field coupled problems with monolithic schemes. Comput Methods Appl Mech Eng. 2016;310:335–66. https://doi.org/10.1016/j.cma.2016.07.016.
Wiesner TA., Gee MW, Prokopenko A, Hu J.: The MueLu Tutorial. Technical Report SAND2014-18624 R, Sandia National Laboratories, Albuquerque, NM (USA) 87185 2014.
Berger-Vergiat L, Glusa CA, Hu JJ, Mayr M, Prokopenko A, Siefert CM, Tuminaro RS, Wiesner TA.: MueLu User’s Guide. Technical Report SAND2019-0537, Sandia National Laboratories, Albuquerque, NM (USA) 87185. 2019. https://www.osti.gov/servlets/purl/1491860.
Berger-Vergiat L, Glusa CA, Hu JJ, Mayr M, Prokopenko A, Siefert CM, Tuminaro RS, Wiesner TA.: MueLu multigrid framework. https://trilinos.github.io/muelu.html. 2019.
Muddle RL, Mihajlović M, Heil M. An efficient preconditioner for monolithically-coupled large-displacement fluid-structure interaction problems with pseudo-solid mesh updates. J Comput Phys. 2012;231(21):7315–34.
Crosetto P, Deparis S, Fourestey G, Quarteroni A. Parallel algorithms for fluid–structure interaction problems in haemodynamics. SIAM J Sci Comput. 2011;33(4):1598–622. https://doi.org/10.1137/090772836.
Deparis S, Forti D, Grandperrin G, Quarteroni A. FaCSI: a block parallel preconditioner for fluid-structure interaction in hemodynamics. J Comput Phys. 2016;327:700–18. https://doi.org/10.1016/j.jcp.2016.10.005.
Mayr M, Wall WA, Gee MW. Adaptive time stepping for fluid–structure interaction solvers. Finite Elements Anal Des. 2018;141:55–69. https://doi.org/10.1016/j.finel.2017.12.002.
Mayr M.: A Monolithic Solver for Fluid-Structure Interaction with Adaptive Time Stepping and a Hybrid Preconditioner. Ph. D. thesis, Technische Universität München. 2016.
Brooks AN, Hughes TJR. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput Methods Appl Mech Eng. 1982;32(1):199–259. https://doi.org/10.1016/0045-7825(82)90071-8.
Hughes TJR, Franca LP, Balestra M. A new finite element formulation for computational fluid dynamics: V. Circumventing the Babuška-Brezzi condition: a stable Petrov-Galerkin formulation of the stokes problem accommodating equal-order interpolations. Comput Methods Appl Mech Eng. 1986;59(1):85–99. https://doi.org/10.1016/0045-7825(86)90025-3.
de Mulder T. The role of bulk viscosity in stabilized finite element formulations for incompressible flow: a review. Comput Methods Appl Mech Eng. 1998;163(1–4):1–10. https://doi.org/10.1016/S0045-7825(98)00015-2.
Gravemeier V, Gee MW, Kronbichler M, Wall WA. An algebraic variational multiscale-multigrid method for large eddy simulation of turbulent flow. Comput Methods Appl Mech Eng. 2010;199(13–16):853–64. https://doi.org/10.1016/j.cma.2009.05.017.
Klöppel T, Popp A, Küttler U, Wall WA. Fluid-structure interaction for non-conforming interfaces based on a dual mortar formulation. Comput Methods Appl Mech Eng. 2011;200(45–46):3111–26.
Wohlmuth BI. A mortar finite element method using dual spaces for the Lagrange multiplier. SIAM J Numer Anal. 2000;38(3):989–1012. https://doi.org/10.1137/S0036142999350929.
Quarteroni A, Valli AMP. Domain decomposition methods for partial differential equations. Oxford: Clarendon; 2005.
Smith B, Bjørstad P, Gropp W. Domain decomposition: parallel multilevel methods for elliptic partial differential equations. Cambridge: Cambridge University Press; 2008.
Toselli A, Widlund OB.: Domain Decomposition Methods: Algorithms and Theory. Springer Series in Computational Mathematics, vol. 34. Springer, Berlin / Heidelberg. 2005.
Chow E, Patel A. Fine-grained parallel incomplete LU factorization. SIAM J Sci Comput. 2015;37(2):169–93. https://doi.org/10.1137/140968896.
Meijerink JA, van der Vorst HA. An iterative solution method for linear systems of which the coefficient matrix is a symmetric \(m\)-matrix. Math Comput. 1977;31(1):148–62. https://doi.org/10.1090/S0025-5718-1977-0438681-4.
Saad Y. Iterative methods for sparse linear systems. Philadelphia: SIAM; 2003.
Gerbeau J-F, Vidrascu M. A quasi-Newton algorithm based on a reduced model for fluid-structure interaction problems in blood flows. ESAIM Math Modell Numer Anal. 2003;37(4):631–47. https://doi.org/10.1051/m2an:2003049.
Deparis S, Forti D, Gervasio P, Quarteroni A. INTERNODES: an accurate interpolation-based method for coupling the Galerkin solutions of PDEs on subdomains featuring non-conforming interfaces. Comput Fluids. 2016;141:22–41. https://doi.org/10.1016/j.compfluid.2016.03.033.
Deparis S, Forti D, Quarteroni A. A fluid–structure interaction algorithm using radial basis function interpolation between non-conforming interfaces. In: Bazilevs Y, Takizawa K, editors. Advances in Computational Fluid–structure interaction and flow simulation. Modeling and simulation in science, engineering and technology. Cham: Springer; 2016. https://doi.org/10.1007/978-3-319-40827-9_34.
Forti D.: Parallel algorithms for the solution of large-scale fluid–structure interaction problems in hemodynamics. Ph. D. Thesis, Ecole Polytechnique Federale de Lausanne, Lausanne, CH. 2016.
Badia S, Nobile F, Vergara C. Robin-Robin preconditioned Krylov methods for fluid–structure interaction problems. Comput Methods Appl Mech Eng. 2009;198(33–36):2768–84. https://doi.org/10.1016/j.cma.2009.04.004.
Deparis S, Discacciati M, Fourestey G, Quarteroni A. Fluid–structure algorithms based on Steklov–Poincaré operators. Comput Methods Appl Mech Eng. 2006;195(41—-43):5797–812. https://doi.org/10.1016/j.cma.2005.09.029.
Dettmer WG, Perić D. A new staggered scheme for fluid-structure interaction. Int J Numer Methods Eng. 2013;93(1):1–22.
Fernández MA, Moubachir M. A Newton method using exact jacobians for solving fluid-structure coupling. Comput Struct. 2005;83(2–3):127–42.
Fernández MA, Gerbeau J-F, Grandmont C. A projection semi-implicit scheme for the coupling of an elastic structure with an incompressible fluid. Int J Numer Methods Eng. 2007;69(4):794–821. https://doi.org/10.1002/nme.1792.
Fernández MA, Mullaert J, Vidrascu M. Explicit Robin-Neumann schemes for the coupling of incompressible fluids with thin-walled structures. Comput Methods Appl Mech Eng. 2013;267:566–93. https://doi.org/10.1016/j.cma.2013.09.020.
Bazilevs Y, Calo VM, Zhang Y, Hughes TJR. Isogeometric fluid–structure interaction analysis with applications to arterial blood flow. Comput Mech. 2006;38(4–5):310–22. https://doi.org/10.1007/s00466-006-0084-3.
de Souza Neto EA, Perić D, Dutko M, Owen DRJ. Design of simple low order finite elements for large strain analysis of nearly incompressible solids. Int J Solids Struct. 1996;33(20—-22):3277–96. https://doi.org/10.1016/0020-7683(95)00259-6.
Boman EG, Çatalyürek UV, Chevalier C, Devine KD. The Zoltan and Isorropia parallel toolkits for combinatorial scientific computing: partitioning. Ordering and coloring. Sci Program. 2012;20(2):29–150. https://doi.org/10.3233/SPR-2012-0342.
Gee MW, Siefert CM, Hu JJ, Tuminaro RS, Sala MG.: ML 5.0 Smoothed Aggregation User’s Guide. Technical Report SAND2006-2649, Sandia National Laboratories, Albuquerque, NM (USA) 87185. 2006.
Förster C.: Robust methods for fluid-structure interaction with stabilised finite elements. PhD thesis, Universität Stuttgart, Stuttgart. 2007.
Holzapfel GA. Nonlinear solid mechanics: a continuum approach for engineering. Chichester: Wiley; 2000.
Chung J, Hulbert GM. A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-\(\alpha \) method. J Appl Mech. 1993;60(2):371–5.
Jansen KE, Whiting CH, Hulbert GM. A generalized-\(\alpha \) method for integrating the filtered Navier–Stokes equations with a stabilized finite element method. Comput Methods Appl Mech Eng. 2000;190(3–4):305–19.
Wall WA.: Fluid–Struktur–Interaktion mit stabilisierten Finiten Elementen. PhD thesis, Universität Stuttgart, Institut für Baustatik, Stuttgart. 1999.
Yoshihara L, Coroneo M, Comerford A, Bauer G, Klöppel T, Wall WA. A combined fluid–structure interaction and multi-field scalar transport model for simulating mass transport in biomechanics. Int J Numer Methods Eng. 2014;100(4):277–99. https://doi.org/10.1002/nme.4735.
Koshiba N, Ando J, Chen X, Hisada T. Multiphysics simulation of blood flow and LDL transport in a porohyperelastic arterial wall model. J Biomech Eng. 2006;129(3):374–85. https://doi.org/10.1115/1.2720914.
Thon MP, Hemmler A, Mayr M, Glinzer A, WIldgruber M, Zernecke-Madsen A, Gee MW. A multiphysics approach for modeling early atherosclerosis. Biomech Model Mechanobiol. 2018;17(3):617–44. https://doi.org/10.1007/s10237-017-0982-7.
Reynolds DR, Gardner DJ, Hindmarsh AC, Woodward CS, Sexton JM.: User Documentation for ARKode v1.0.2 (SUNDIALS v2.6.2). Technical Report LLNL-SM-668082, Lawrence Livermore National Laboratory. 2015.
Kelley CT. Solving nonlinear equations with Newton’s method. Philadelphia: Fundamentals of algorithms. SIAM; 2003.
Acknowledgements
This work was mostly performed while the author was at the Mechanics & High Performance Computing Group, Technical University of Munich, Parkring 35, 85748 Garching b. München..
Funding
This work was supported by the Leibniz Rechenzentrum München (LRZ) of the Bavarian Academy of Sciences under contract number pr48ta. LRZ provided computing resources and software engineering support. LRZ has no part in the design of this study or the writing of this manuscript.
Author information
Authors and Affiliations
Contributions
MM developed the idea, conducted numerical experiments, and wrote the manuscript. MHN contributed to the software implementation and to the second numerical example. MWG fine-tuned the research idea, suggested numerical experiments, and revised the paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Convergence checks for iterative monolithic linear and Nonlinear solvers for coupled problems
Appendix A: Convergence checks for iterative monolithic linear and Nonlinear solvers for coupled problems
Appropriate stopping criteria have to be provided for both the iterative linear and nonlinear solver. Thereby, common norms are Euclidian vectors norms, namely the length-scaled 2-norm \(\left\| \left( \bullet \right) \right\| _{2}\) and the \(\mathrm {inf}\)-norm \(\left\| \left( \bullet \right) \right\| _{\infty }\), which are given as
with \(k=1,\ldots ,K\) and K being the number of entries in the vector \(\left( \bullet \right) \).
A. 1 Convergence check for the nonlinear solver
In the context of solving a system of nonlinear equations, the stopping criterion is usually based on the comparison of a norm of the nonlinear residual vector \(\mathbf {r}\) to a user-given tolerance \(\varepsilon ^\mathrm {nln}_{\mathbf {r}}\). The stopping criterion is satisfied if
The norm of the solution increment can be included in the convergence check via additionally asking for
For both convergence checks, 2-norm and \(\mathrm {inf}\)-norm are applicable. In this work, we base the nonlinear convergence check on absolute norms. In practical applications, often weighted norms [60] or a combination of absolute and relative tolerance [61] seem to be useful.
In multi-physics applications like the FSI problem at hand, both the global solution and residual vector are assembled based on solution and residual vectors of each field involved in the problem, cf. e.g. (1) for the global FSI residual. However, there is no guarantee that the portions from each field are somehow balanced, neither w.r.t. size of the vectors nor w.r.t. their magnitude. It may happen—and this is usually the case—that solid and fluid field differ significantly in size and magnitude of their residual vectors. While differences in size are due to geometric dimensions and spatial discretization, discrepancy in magnitude can have several reasons. On the one hand, different systems of units may be used in both fields, but even with the same system of units differences in physical properties may lead to differences in the magnitude of the residual vector. On the other hand, the initial residual vector depends on the initial guess of the solution vector. This initial guess can be of varying quality in both fields, which might lead to a small residual contribution of one field, if its initial guess is very good, whereas the other field exhibits a large residual due to a less accurate initial guess.
Having in mind the possibly huge variations of the contributions to the global residual vector, it seems to be inadvisable to judge about convergence based on norms of the global residual vector, only. Especially when using a 2-norm, the residual norm might be dominated by one of the fields such that no control over the other fields can be guaranteed. This dominating effect can be either based on the length scaling included in the 2-norm or based on the different magnitudes of the field residuals. Even the application of the \(\mathrm {inf}\)-norm might be problematic since choosing a single tolerance does not reflect for possible variations in magnitude of the field residuals. Similar arguments hold for testing the solution increment vector.
To circumvent these issues, a more sophisticated convergence check is performed that reflects the contributions of the different physical fields as well as the coupling between them. The nonlinear monolithic residual as well as the monolithic solution increment vector are decomposed into physics-based portions, namely
all entries related to the solid’s displacement degrees of freedom:
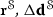
all entries related to the fluid’s velocity degrees of freedom:
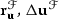
all entries related to the fluid’s pressure degrees of freedom:
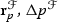
all entries related to the fluid-structure interface:
 with
with  depending on the choice of master and slave side in the mortar coupling
depending on the choice of master and slave side in the mortar coupling
For each of these physics-based portions, both 2-norm and \(\mathrm {inf}\)-norm are required to satisfy user-given tolerances that may be different for each vector portion. To achieve convergence, all individual tests must be passed at the same time, which is equivalent to tie all individual tests together with a logical AND relation.
Choosing all these tolerances is up to the user. The computational engineer can select meaningful tolerances, where the influence of the system of units, the problem size, and the desired accuracy need to be taken into account. Usually, physical insight into the problem is helpful. General rules cannot be provided. A possible strategy is outlined in [60].
A. 2 Convergence check for the linear solver
The linear system of equations is solved with the preconditioned GMRES method [12]. Convergence is tested by means of a relative residual norm, reading
with \(\left\| \mathbf {r}_{\mathrm {lin}}^{i}\right\| _{2}\) denoting the 2-norm of the linear residual in GMRES iteration \(i\) which is normalized with the initial residual norm \(\left\| \mathbf {r}_{\mathrm {lin}}^{0}\right\| _{2}\). The base tolerance \(\varepsilon ^\mathrm {lin}\) is given by the user with typical values being in the range of \(10^{-4}-10^{-5}\). Its interplay with the nonlinear convergence tolerances needs to be considered to obtain a reasonable value.
With progress of the nonlinear solver, the nonlinear residual \(\mathbf {r}^{k}\) is likely to consist of small entries, which might approach the limit of machine precision. In such scenarios, it might be very expensive or even unfeasible to converge the linear solver to its base tolerance \(\varepsilon ^\mathrm {lin}\). This is remedied by adapting the convergence test to
The scalar factor \(\beta ^\mathrm {lin}\) is usually chosen in the range of \(10^{-2}-10^{-3}\). It loosens the effective tolerance for the linear convergence check in case that the nonlinear residual norm \(\left\| \mathbf {r}^{k}\right\| _{2}\) is smaller than \(\beta ^\mathrm {lin}\), such that the linear solver is required to converge to a tolerance that is less tight with ongoing convergence of the nonlinear solver. This strategy saves computational time and avoids aiming at accuracies in the linear solver that are infeasible to achieve.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mayr, M., Noll, M.H. & Gee, M.W. A hybrid interface preconditioner for monolithic fluid–structure interaction solvers. Adv. Model. and Simul. in Eng. Sci. 7, 15 (2020). https://doi.org/10.1186/s40323-020-00150-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40323-020-00150-9









 is prescribed in
is prescribed in 

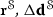
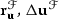
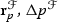
 with
with  depending on the choice of master and slave side in the mortar coupling
depending on the choice of master and slave side in the mortar coupling