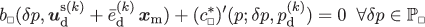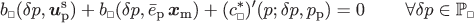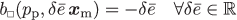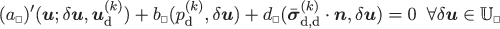- Research Article
- Open access
- Published:
On the variationally consistent computational homogenization of elasticity in the incompressible limit
Advanced Modeling and Simulation in Engineering Sciences volume 2, Article number: 1 (2015)
Abstract
Background
Computational homogenization is a well-established approach in material modeling with the purpose to account for strong micro-heterogeneity in an approximate fashion without excessive computational cost. However, the case of macroscopically incompressible response is still unresolved.
Methods
The computational framework for Variationally Consistent Homogenization (VCH) of (near) incompressible solids is discussed. A canonical formulation of the subscale problem, pertinent to a Representative Volume Element (RVE), is established, whereby complete macroscale incompressibility is obtained as the limit situation when all constituents are incompressible.
Results
Numerical results for single RVEs demonstrate the seamless character of the computational algorithm at the fully incompressible limit.
Conclusions
The suggested framework can seamlessly handle the transition from (macroscopically) compressible to incompressible response. The framework allows for the classical boundary conditions on the RVE as well as the generalized situation of weakly periodic boundary conditions.
Background
Computational homogenization is a well-established approach in material modeling with the purpose to account for strong micro-heterogeneity in an approximate fashion without excessive computational cost. Such an approach can be applied to the situation when the intrinsic material properties are linear, leading to direct “upscaling”. It can also be applied to the more complex situation when the subscale properties are nonlinear and/or the subscale problem is inherently transient, whereby it is necessary to resort to nested macro-subscale computation (FE2). Since the literature on classical as well as computational homogenization is abundant, it is neither necessary nor possible to give a comprehensive account. Selected references are [1-3] addressing different aspects on homogenization and multiscale modeling. An important issue is the choice of boundary conditions (and data) for the subscale RVE-problem. Selected references are [4-8]. In particular, [8] presents a quite general framework based on “weak periodicity”. How to accommodate the coalescence of microcracks presents a special challenge, e.g. [9]. How to incorporate interfaces and thin membranes are discussed in [10-12].
Despite the extensive developments, there are still fundamental issues that need to be further addressed. Among these issues we note, (i) variational consistency and the macrohomogeneity condition in the context of selective homogenization (in particular, for multi-field problems) (cf. [13,14]), (ii) how to establish bounds on the effective properties within a given confidence interval, and (iii) high contrast material properties of the constituents (e.g. rigid inclusions or pores) for which the classical Dirichlet and Neumann conditions give poor results.
The particular aspect considered in this paper, which represents an unresolved issue even in the simplest case of elastic response, is that of Variationally Consistent Homogenization (VCH) in the limit of macroscopic incompressibility. This situation is encountered when the micro-constituents of a composite are intrinsically incompressible (or nearly incompressible), which infers macroscale incompressibility as well. An example is when a composite of metallic particles (or fibers) embedded in an elastomer matrix is subjected to stresses that are sufficiently large to cause significant plastic deformations in the particles. Another class of problems is characterized by an initially compressible macroscale response, which may become incompressible as the result of the deformation process. An important example is the evolving porous microstructure of a PM-product during the process of sintering, whereby the homogenized response is compressible until the porosity vanishes inferring incompressible macroscale response, cf. [15]. This process is thus characterized by a transition from the compressible to incompressible regimes.
Applying traditional deformation controlled boundary conditions to macroscopically incompressible RVEs is technically possible, see e.g. Moran et al. [16] and Öhman et al. [14]. However, in such cases, special care must then be taken in applying compatible deformations (i.e. no scaling). This leads to a singular, but solvable, RVE-problem. This approach, however, raises three significant issues: (i) FE2 is only possible with approximate penalty methods, (ii), the situations of macroscopically compressible and incompressible response require different solution strategies, (iii) the average pressure is not coupled between the scales. One attempt to adress these issues based on a mixed variational framework, was presented by Öhman et al. [17]. In this paper, an alternative formulation is presented, where the mixed variational format on the macroscale is derived directly via homogenization. As compared to [17], extension is also made to weakly periodic boundary condition for the RVE.
The paper is outlined as follows: The appropriate variational setting of the fine-scale elasticity problem in a mixed format is given. Next, the corresponding VCH framework and macroscale problem are outlined. The canonical form of the RVE-problem, based on weakly periodic boundary conditions is established, followed by the Dirichlet and Neumann type boundary conditions resulting in upper and lower bounds on the RVE response. Numerical examples of RVE-problems are then shown, followed by conclusions.
Methods
Subscale modeling of isotropic elasticity allowing for the incompressible limit
A mixed displacement-pressure weak format
We consider a generic micro-heterogeneous, i.e. polycrystalline, material in a given body whose macroscopic configuration occupies the region Ω in space with (presumed smooth) boundary Γ. We are then lead to defining a Representative Volume Element (RVE), that represents the topology of the micro-heterogeneous microstructure, as shown in Figure 1. The total domain occupied by the cubic RVE is denoted  with external boundary
with external boundary  .
.
We consider a model material as follows: The stress is decomposed in terms of deviator and pressure as σ=σ d−p I where \(p \overset {\text {def}}{=} -\frac 13\text {tr}(\boldsymbol {\sigma }\!)\), and the strain is decomposed in terms of deviator and dilation as \(\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\mathrm {d}} + \frac {1}{3} e\boldsymbol {I}\) where \(e\overset {\text {def}}{=} \text {tr}(\boldsymbol {\epsilon }) = \boldsymbol {u} \cdot \boldsymbol {\nabla }\). With the kinematic definition \(\boldsymbol {\epsilon }_{\mathrm {d}}[\!\boldsymbol {u}]\overset {\text {def}}{=} \,[\!\boldsymbol {u}\otimes \boldsymbol {\nabla }]^{\text {sym}}-\frac {1}{3}[\!\boldsymbol {u}\cdot \boldsymbol {\nabla }]\boldsymbol {I}\), we introduce the constitutive relations
Hence, \(\hat {\boldsymbol {\sigma }}_{\mathrm {d}}(\bullet)\) and \(\hat {e}(\bullet)\) denote suitable constitutive functions. Obviously, in the simplest case of linear isotropic elasticity, we have \(\hat {\boldsymbol {\sigma }}_{\mathrm {d}}(\boldsymbol {\epsilon }_{\mathrm {d}})=2G\boldsymbol {\epsilon }_{\mathrm {d}}\) and \(\hat {e}(p)=-\frac {1}{K}p\), where G(x),K(x) for x∈Ω are the standard elastic moduli that fluctuate strongly. Moreover, intrinsic incompressibility is defined as \(\hat {e}(p)=0\) for any value of p. We are now in the position to formulate the strong format of the fine-scale problem under standard quasistatic conditions and small strain kinematics:
The corresponding weak format is: Find \(\boldsymbol {u}\in \mathbb {U}, p\in \mathbb {P}\) s.t.
where
The solution space  and the test space \(\mathbb {U}^{0}\) are defined in standard fashion. In particular, all \(\boldsymbol {v}\in \mathbb {U}\) are characterized by v=u
pre on Γ
D, whereas all \(\boldsymbol {v}\in \mathbb {U}^{0}\) satisfy v=0 on Γ
D. The pressure space
and the test space \(\mathbb {U}^{0}\) are defined in standard fashion. In particular, all \(\boldsymbol {v}\in \mathbb {U}\) are characterized by v=u
pre on Γ
D, whereas all \(\boldsymbol {v}\in \mathbb {U}^{0}\) satisfy v=0 on Γ
D. The pressure space  does not satisfy any boundary conditions.
does not satisfy any boundary conditions.
It is illuminating (although not necessary from an operational point of view) to invoke the potential Π(u,p)
where ψ u (ε d) and \(\psi _{p}^{*}(p)\) are constitutive energy densitiesa such that
The stationarity conditions of Π(u,p) are
which are identical to the weak form in (3).
Variationally Consistent Homogenization
VMS-ansatz and scale separation
The appropriate variational setting of the homogenized problem is obtained upon replacing the integrands in the weak forms in (4)–(7) by running averages of the type

representing a smoothing approximation on a RVE. In practice, the RVE’s are finite-sized and occupies the subscale region  with boundary
with boundary  . The typical dimension of an RVE is
. The typical dimension of an RVE is  . The RVE is centered at the macroscale position
. The RVE is centered at the macroscale position  for any given \(\bar {\boldsymbol {x}}\in \Omega \). Boundary integrals can be homogenized in similar fashion, by considering Representative Surface Elements Γ
#
for any given \(\bar {\boldsymbol {x}}\in \Omega \). Boundary integrals can be homogenized in similar fashion, by considering Representative Surface Elements Γ
#
The weak forms in (4)–(7) are thus approximated as




where the RVE-functionals in (13)–(16) are defined as




Likewise, we homogenize the volume-specific energy potential Λ(u,p):

where the RVE-functional  is given as
is given as

In the spirit of the Variational MultiScale method (VMS) [18], we introduce the ansatz that the fields \(\boldsymbol {u}\in \mathbb {U}\) and \(p\in \mathbb {P}\) can be decomposed into macroscale (smooth) and subscale (fluctuating) parts inside each RVE via the unique hierarchical split \(\mathbb {U} = \mathbb {U}^{\mathrm {M}} \oplus \mathbb {U}^{\mathrm {s}}\) and \(\mathbb {P} = \mathbb {P}^{\mathrm {M}} \oplus \mathbb {P}^{\mathrm {s}}\). As a result, we may assume that it is possible to solve for the fluctuation fields \(\boldsymbol {u}^{\mathrm {s}}\in \mathbb {U}^{\mathrm {s}}\) and \(p^{\mathrm {s}}\in \mathbb {P}^{\mathrm {s}}\) as “local approximations” on each RVE for given macroscale solutions \(\boldsymbol {u}^{\mathrm {M}}\in \mathbb {U}^{\mathrm {M}}\) and \(p^{\mathrm {M}}\in \mathbb {P}^{\mathrm {M}}\), i.e. we construct the complete solution on each RVE asb.


On the boundary of the macroscale domain, Γ, we assume smooth variation of u defined by the explicit relations u=u M, p=p M on Γ # .
In addition, the test function \(\delta \boldsymbol {u}\in \mathbb {U}^{0}\) in (3a) is replaced by \(\delta \boldsymbol {u}^{\mathrm {M}}\in \mathbb {U}^{{\mathrm {M}},0}\), whereas \(\delta p\in \mathbb {P}\) in (3b) is replaced by \(\delta p^{\mathrm {M}}\in \mathbb {P}^{\mathrm {M}}\). Altogether, these assumptions infer that \(\boldsymbol {u}^{\mathrm {M}}\in \mathbb {U}^{\mathrm {M}}\) and \(p^{\mathrm {M}}\in \mathbb {P}^{\mathrm {M}}\) can be solved from the homogenized problem
Explicit format of macroscale (homogenized) problem
In practice, the scales are linked by expressing \(\boldsymbol {u}^{\mathrm {M}}(\bar {\boldsymbol {x}},{\boldsymbol {x}})\)
c and \(p^{\mathrm {M}}(\bar {\boldsymbol {x}},\boldsymbol {x})\) using Taylor series expansions of suitable order for \(\bar {\boldsymbol {x}}\in \Omega \) and  in terms of the macroscale solution \(\bar {\boldsymbol {u}}(\bar {\boldsymbol {x}})\) and \(\bar {p}(\bar {\boldsymbol {x}})\) respectively. We thus introduce the macroscale fields \((\bar {\boldsymbol {u}},\bar {p})\in \bar {\mathbb {U}}\times \bar {\mathbb {P}}\) such that the macroscale solutions u
M,p
M inside each RVE are expanded as follows:
in terms of the macroscale solution \(\bar {\boldsymbol {u}}(\bar {\boldsymbol {x}})\) and \(\bar {p}(\bar {\boldsymbol {x}})\) respectively. We thus introduce the macroscale fields \((\bar {\boldsymbol {u}},\bar {p})\in \bar {\mathbb {U}}\times \bar {\mathbb {P}}\) such that the macroscale solutions u
M,p
M inside each RVE are expanded as follows:


Hence, u
M is assumed to have linear variation in  pertinent to standard “first order homogenization”, whereas p
M is constant in
pertinent to standard “first order homogenization”, whereas p
M is constant in  . Now, we require that
. Now, we require that


which leads to the constraints


As a result, the hierarchical split (\(\mathbb {U} = \mathbb {U}^{\mathrm {M}} \oplus \mathbb {U}^{\mathrm {s}}\) and \(\mathbb {P} = \mathbb {P}^{\mathrm {M}} \oplus \mathbb {P}^{\mathrm {s}}\)) is guaranteed.
We can thus establish at the outset, before any further analysis, that the displacement and pressure fields within each RVE are implicit functions of the values \(\bar {\boldsymbol {u}}\), \(\bar {\boldsymbol {h}}\), \(\bar {p}\), such that \(\boldsymbol {u} = \tilde {\boldsymbol {u}}\{\bar {\boldsymbol {u}}, \bar {\boldsymbol {h}}, \bar {p}\}\) and \(p = \tilde {p}\{\bar {\boldsymbol {u}}, \bar {\boldsymbol {h}}, \bar {p}\}\).
With the representations in (25) and the constraints in (26) and (27), we are in the position to compute the homogenized quantities that enter the system (24):






The applied macroscale loads \(\bar {\boldsymbol {f}}\), \(\bar {\boldsymbol {t}}_{\text {pre}}\) and “moments” \(\,\bar {\bar {\boldsymbol {f}}}\), \(\bar {\bar {\boldsymbol {t}}}_{\text {pre}}\) are defined as


Remark.
Henceforth, we restrict to the situation when  and |Γ
#
|→0; hence \(\bar {\bar {\boldsymbol {f}}}\) and \(\bar {\bar {\boldsymbol {t}}}_{\text {pre}}\) will vanish. We will also focus on the homogenization of \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\), so \(\bar {\boldsymbol {f}}\) and \(\bar {\boldsymbol {t}}_{\text {pre}}\) are considered as given macroscopic quantities.
and |Γ
#
|→0; hence \(\bar {\bar {\boldsymbol {f}}}\) and \(\bar {\bar {\boldsymbol {t}}}_{\text {pre}}\) will vanish. We will also focus on the homogenization of \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\), so \(\bar {\boldsymbol {f}}\) and \(\bar {\boldsymbol {t}}_{\text {pre}}\) are considered as given macroscopic quantities.
The variationally consistent macroscale “flux” variables \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\) are obtained from homogenization of the constitutive functions as follows:

By combining (23) with (25) we note that \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\) are indeed implicit functions of the values of the macroscale variables \(\bar {\boldsymbol {u}}\), \(\bar {\boldsymbol {h}}\) and \(\bar {p}\), pertinent to the considered RVE.
Finally, upon inserting (28)–(33) into the system (24), we obtain the macroscale problem: Find \((\bar {\boldsymbol {u}},\bar {p})\in \bar {\mathbb {U}}\times \bar {\mathbb {P}}\) that solve
where
If we consider the macroscale fields, \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\), we conclude that they are implicit functions of the fields \(\bar {\boldsymbol {u}}\) and \(\bar {p}\). The macroscale spaces \(\bar {\mathbb {U}}\) and \(\bar {\mathbb {P}}\) are chosen as the standard ones for the fine-scale problem.
Canonical formulation of RVE-problem
Preliminaries – Concept of weak periodicity of fluctuation displacement
To avoid unnecessary technical complexity, we henceforth consider the situation without volume load, i.e. f=0. As a preliminary for establishing the proper variational format of the RVE-problem, we consider the most general weak form of the quasi-static momentum balance by introducing the boundary integral with boundary tractions:


or, more explicitly,


which is supposed to hold true for all possible δ u,δ p in suitable function spaces (as discussed below). However, this problem is not solvable without further specification of the solution fields u,p,t. In this paper we adopt a recently proposed variational framework allowing for weak satisfaction of micro-periodicity, cf. Larsson et al. [8], and this framework will be briefly summarized in what follows. We then assume that the subscale fluctuation field u s is periodic across the RVE boundaries w.r.t. the chosen local coordinate axes. This model assumption, which may be termed “micro-periodicity”, is a key ingredient (and frequently adopted) in the literature on mathematical homogenization and can be viewed as an approximation between the stiffer Dirichlet and the weaker Neumann boundary conditions. Indeed, both these cases can be obtained as special cases of the most general variational format of periodicity (as will be discussed further below).
In order to formulate the conditions on micro-periodicity, we consider the RVE in Figure 2, where the boundary  has been split into two parts:
has been split into two parts:  . Here,
. Here,  is the image boundary (later chosen as the computational domain for boundary integration), whereas
is the image boundary (later chosen as the computational domain for boundary integration), whereas  is the mirror boundary. We shall now introduce the proper mapping
is the mirror boundary. We shall now introduce the proper mapping  such that any point
such that any point  is mirrored in a self-similar fashion to the corresponding point
is mirrored in a self-similar fashion to the corresponding point  ; hence, x
−=φ
per(x
+).
; hence, x
−=φ
per(x
+).
In particular, we express micro-periodicity of the displacement fluctuation field as

or, equivalently, in terms of the “jump” between the fluctuation fields on the image and mirror parts of the boundary as follows:

Subsequently, we shall not enforce the condition (45) strongly as the point of departure; rather it is done weakly. To this end, we assume that the boundary tractions \(\boldsymbol {t}\overset {\text {def}}{=}\boldsymbol {\sigma }\cdot \boldsymbol {n}\) satisfy the following anti-symmetry condition for any regular mirror point

as depicted in Figure 2. We now evaluate, upon using (46), the boundary term in (42a) and (43a), as follows:

A weak statement of the micro-periodicity constraint, given in strong form in (46), is

where the space of test functions that “live” only on the image boundary  is given as
is given as  .
.
RVE-problem – Original “variationally consistent” weak format
In order to establish the most straightforward formulation of the RVE-problem, based on micro-periodicity, we first use the constraints in (27) and introduce the following spaces for the fluctuation fields:


It is then obvious that, for given macroscale values \(\bar {\boldsymbol {u}}\), \(\bar {\boldsymbol {h}}\), and \(\bar {p}\), we can introduce the unique decompositions


Next, we aim for a unique decomposition of the tractions (which are anti-periodic by assumption) in a fashion that is similar to (51). To this end, we first associate each traction field t along  with the average stress \(\bar {\boldsymbol {\tau }}[\!\boldsymbol {t}] \in \mathbb {R}^{3\times 3}\), defined as
with the average stress \(\bar {\boldsymbol {\tau }}[\!\boldsymbol {t}] \in \mathbb {R}^{3\times 3}\), defined as

This definition for the average stress is chosen so that for any stress field τ in equilibrium and such that t=τ·n on  we obtain
we obtain  . We also conclude that
. We also conclude that

As a direct consequence of (52), we may introduce the unique split

where  is the space of the traction fluctuations that are self-equilibrating and thus defined as
is the space of the traction fluctuations that are self-equilibrating and thus defined as

The proof of uniqueness of the split in (54) follows from the identity
and the fact that
Hence,  . □
. □
As preliminaries for establishing the RVE-problem, we establish two identities: Firstly, from (53) and (54) follows that

Secondly, it follows from (25a) and the properties of  that
that

whereby it is noted that the macroscale part of u is “filtered out”.
We are now in the position to establish the subscale problem: For given values \(\bar {\boldsymbol {u}}\), \(\bar {\boldsymbol {h}}\), and \(\bar {p}\), that represent the macroscale fields (and which solve the macroscale problem), find the subscale fluctuations  that solve the system
that solve the system



where the RVE-functionals were introduced in (17)–(19) and (48).
By inspecting the system in (60), we note that it is not the entire \(\bar {\boldsymbol {h}}\) that is used as input to the RVE-problem. In fact, it is readily concluded that it is only the deviatoric part \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}=\bar {\boldsymbol {h}}^{\text {sym}}_{\mathrm {d}}\) that enters as “data” to the RVE-problem. In other words, neither \(\bar {\boldsymbol {u}}\), the volumetric part \(\bar {h}_{\mathrm {v}}\overset {\text {def}}{=}\bar {\boldsymbol {h}}:\boldsymbol {I}\), nor the skew-symmetric part \(\bar {\boldsymbol {h}}^{\text {skw}}=\frac {1}{2}\!\left [\bar {\boldsymbol {h}}-\bar {\boldsymbol {h}}^{\mathrm {T}}\right ]\) will affect the RVE-solution. In conclusion, (\(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}},\bar {p})\) are the macroscale variables that are used as data for the RVE-problem; hence, the solution of (60) is parameterized as \(\boldsymbol {u}^{\mathrm {s}}=\boldsymbol {u}^{\mathrm {s}}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\), \(p^{\mathrm {s}}=p^{\mathrm {s}}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\), and \(\boldsymbol {t}^{\mathrm {s}}=\boldsymbol {t}^{\mathrm {s}}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\). In a postprocessing step the homogenized “fluxes” can be represented as


Note that \(\bar {e}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\neq \bar {h}_{\mathrm {v}}\) in general!
From the aforesaid, it appears that there is a problem associated with the presented “consistent” format in the sense that the strong form of the continuity equation does not (necessarily) represent that one of the fine scale. The reason is that the formulation (60b) “filters out” any imposed constant volumetric strain \(\bar {\lambda }\); hence, the strong format generally reads
Clearly, testing (62) with a constant pressure, we obtain  .
.
Remark.
In the special case of intrinsically incompressible material response, defined by \(\hat {e}(p)=0\) in  , for any p, then we have
, for any p, then we have  . However, from (60b), (60c) it is concluded that the solution of the RVE-problem is
. However, from (60b), (60c) it is concluded that the solution of the RVE-problem is  , whereby we obtain \(\bar {\lambda }=\bar {h}_{\mathrm {v}} \neq 0\). It is only when the macroscale solution represents incompressible response, i.e. when \(\bar {h}_{\mathrm {v}} = 0\), that we obtain \(\bar {\lambda } = 0\). In conclusion, the RVE-problem is able to provide an “incompressible solution” even in the case that the macroscale solution represents compressible response. This anomaly is the main motivation for establishing an alternative format of the problem, which is discussed next.
, whereby we obtain \(\bar {\lambda }=\bar {h}_{\mathrm {v}} \neq 0\). It is only when the macroscale solution represents incompressible response, i.e. when \(\bar {h}_{\mathrm {v}} = 0\), that we obtain \(\bar {\lambda } = 0\). In conclusion, the RVE-problem is able to provide an “incompressible solution” even in the case that the macroscale solution represents compressible response. This anomaly is the main motivation for establishing an alternative format of the problem, which is discussed next.
Macrohomogeneity condition (VCMC)
The Variationally Consistent Macrohomogeneity Condition (VCMC) (or generalized Hill-Mandel condition) is reviewed in Appendix ‘Variationally Consistent Homogenization (VCH)’. In order to establish its localized form for the present problem, we first identify the tangent spaces


whereby  and
and  represent sensitivity fields (or directional derivatives) for given changes
represent sensitivity fields (or directional derivatives) for given changes  and
and  of the macroscale fields within each RVE.
of the macroscale fields within each RVE.
The macrohomogeneity condition is satisfied if, for any given state u M, p M localized to the considered RVE, the following relations hold:


In order to show that this condition is, indeed, satisfied automatically by the solution of the RVE-problem as defined in (60), it suffices to consider (60c). Upon differentiating this relation w.r.t. u M and p M, we obtain

for any  (by definition of (u
s)′ {u
M,p
M;du
M,dp
M}). Now choosing δ
t
s=t
s in (65), we obtain
(by definition of (u
s)′ {u
M,p
M;du
M,dp
M}). Now choosing δ
t
s=t
s in (65), we obtain

Finally, upon choosing  in (60a) and
in (60a) and  in (60b) while noting the identity in (66) we recover (64). In conclusion the VCMC is satisfied.
in (60b) while noting the identity in (66) we recover (64). In conclusion the VCMC is satisfied.
Remark.
In the present case there is, obviously, no need to compute the sensitivities du s=(u s)′ and dp s=(p s)′ explicitly. However, it is always possible to compute the sensitivities of all the fluctuation fields, u s, p s, and t s from the (linear) system obtained by linearizing (60). This system is closely related to the sensitivity problem that must be established as part of computing the pertinent macroscale tangent tensors exploited in Newton iterations on the macroscale problem. The explicit format of that sensitivity problem is discussed in Appendix ‘Sensitivity problem’ for the Canonical format of the RVE-problem that is introduced subsequently.
RVE-problem – Canonical weak format
A generalized formulation of the RVE-problem that does not contain the above-mentioned inconsistency with the strong format is considered next. Firstly, we introduce the following spaces for the total (macroscale and fluctuation) fields:



Secondly, the fine-scale fields within an RVE are decomposed as


where \(\boldsymbol {x}_{\mathrm {m}}\overset {\text {def}}{=}\frac {1}{3}[\!\boldsymbol {x}-\bar {\boldsymbol {x}}]\), and where \(\bar {e}\) is an additional scalar quantity which, at the outset, does not depend on the macroscale field(s).
Remark.
As a consequence of the ansatz in (70a), the rigid body motion is removed; \(\bar {\boldsymbol {u}} = \boldsymbol {0}\) and \(\bar {\boldsymbol {h}}^{\text {skw}} = \boldsymbol {0}\). Hence, the ansatz u is not identical to the solution u=u M+u s as expressed in (51a).
We now propose the alternative, subsequently denoted canonical, formulation of the RVE-problem as follows: For given values \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\), \( \bar {p}\), that represent the macroscale fields (which solve the macroscale problem), find the subscale fields  that solve the system
that solve the system




If follows from (72) that the new variable \(\bar {e}\) correctly obtains the value  in accordance with (61b). To show this result, we first use the divergence theorem to obtain the identities
in accordance with (61b). To show this result, we first use the divergence theorem to obtain the identities

Using these identities together with (71b), (71c), we deduce

The solution of the “canonical” problem (71) contains, in fact, the solution of the original “variationally consistent” problem in (60); however, without the apparent drawback that is associated with that format. The fluctuations
are identical to  that solve the system (60). This important result can be shown by introducing the unique split of the unknowns
that solve the system (60). This important result can be shown by introducing the unique split of the unknowns



Firstly, inserting these relations into (71c) and testing with \(\delta \check {\boldsymbol {\tau }}\) we obtain

which gives
Next, testing (71a) with \(\delta \check {\boldsymbol {h}}\) we obtain

which gives
Lastly, from (71d) we obtain

With (81), this result implies that \(\check {p} = \bar {p}\).
Now, testing (71a)–(71c) with the fluctuations δ u s, δ p s, and δ t s respectively, we obtain exactly the original system in (60). Hence, we compute the identical quantities \(\boldsymbol {u}^{\mathrm {s}} \{\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}, \bar {p}\}\) and \(p^{\mathrm {s}}\{\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}, \bar {p}\}\). Finally, the canonical form results in the identical responses \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\) and \(\bar {e}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\) as expressed in (61). Since the macroscopic response variables are identical, the VCMC is still fulfilled.
An illustrative comparison between the two RVE formulations are shown Figure 3. Despite the different displacement fields, the homogenized responses, \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\), are the same.
Remark.
Fine-scale incompressibility within the RVE is defined by  , which gives
, which gives  . As a result,
. As a result,  . In practice, there is (of course) no need to establish s a separate system, since \(\bar {e}=0\) is obtained directly as part of the solution of (71) in this case.
. In practice, there is (of course) no need to establish s a separate system, since \(\bar {e}=0\) is obtained directly as part of the solution of (71) in this case.
Variational properties of the RVE-problem – Energy bounds from RVE-functional
Variational properties for the canonical formulation of the RVE-problem – The RVE-potential
In order to establish bounds on the homogenized properties based on the results from the Dirichlet and Neumann problems, we shall introduce an appropriate “RVE-potential” as follows:

where  is the “intrinsic” energy potential that was defined in (22).
is the “intrinsic” energy potential that was defined in (22).
We now define the volume-specific “macroscale energy density”d as the value of  at the following generalized saddle-point:
at the following generalized saddle-point:

A stationary point of  is defined by the relations
is defined by the relations




It is readily seen that the system in (85) is precisely that of (71), and we may parameterize its solution as
At the stationary point, we may use the result in (85c) to conclude that

whereby the energy at the stationary point is deduced to become

We now deduce that  serves as the “macroscale energy density” for \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\) in the sense that we have the macroscale constitutive relations
serves as the “macroscale energy density” for \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\) in the sense that we have the macroscale constitutive relations

Details of the proof are given in Appendix ‘Homogenized macroscale energy’.
From the solution of the RVE-problem, \(\bar {e}\) is obtained directly as a primary variable. The deviatoric stress \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) is obtained by post-processing:

Variational properties for Dirichlet boundary conditions
In order to establish a suitable variational setting we replace the solution space  with
with  defined as
defined as

where

while  are the same spaces as for the generic problem. The generalized saddle-point problem (84) can now be rephrased as
are the same spaces as for the generic problem. The generalized saddle-point problem (84) can now be rephrased as

where

The only possibility to obtain a finite value of  while evaluating the sup over
while evaluating the sup over  is to set \(\check {\boldsymbol {\epsilon }}_{\mathrm {d}} = \bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\check {e} = \hat {\bar {e}}\). Hence, we replace the saddle-point problem by
is to set \(\check {\boldsymbol {\epsilon }}_{\mathrm {d}} = \bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\check {e} = \hat {\bar {e}}\). Hence, we replace the saddle-point problem by

where

A stationary point of  is defined by the relations
is defined by the relations



and this system of equations takes the explicit form: For given values \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}, \bar {p}\), find the subscale fields  that solve the system
that solve the system



Finally, the macroscale energy density at the stationary point becomes

From the RVE-problem in (98), \(\bar {e}\) is obtained directly as a primary variable. The deviatoric stress \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) is obtained by post-processing:

However in practice \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) is conveniently obtained as the reaction forces associated with the prescribed \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\).
Remark.
The VMCM in (64) is still valid for the restricted space  . Since
. Since  , (64a) is satisfied for all \(\delta \boldsymbol {u}^{\mathrm {s}}\in \mathbb {U}^{{\mathrm {D}},\mathrm {s}}\).
, (64a) is satisfied for all \(\delta \boldsymbol {u}^{\mathrm {s}}\in \mathbb {U}^{{\mathrm {D}},\mathrm {s}}\).
Variational properties for Neumann boundary conditions
The Neumann condition represents the weakest possible way of enforcing the micro-periodicity condition. Here it is considered as a model assumption; however, it is also possible to view this choice as a (crude) FE-approximation of the deviatoric traction field. The pertinent RVE-problem is obtained from the general format upon restricting the space  , i.e. introducing
, i.e. introducing  defined as
defined as

while  and
and  are left unrestricted. Clearly, the choice of
are left unrestricted. Clearly, the choice of  restricts the tractions to become piecewise constant on each of the three positive boundary faces of the RVE-cube. The generalized saddle-point problem (84) can then be rephrased as
restricts the tractions to become piecewise constant on each of the three positive boundary faces of the RVE-cube. The generalized saddle-point problem (84) can then be rephrased as

where

The only possibility to obtain a finite value of  while evaluating the inf over \(\hat {\bar {e}}\in \mathbb {R}\) is to set \(\check {p} = \bar {p}\). As a direct consequence the variable \(\hat {\bar {e}}\) disappears in the resulting expression, cf. (105) below. Moreover, from (90) we see that for tractions
while evaluating the inf over \(\hat {\bar {e}}\in \mathbb {R}\) is to set \(\check {p} = \bar {p}\). As a direct consequence the variable \(\hat {\bar {e}}\) disappears in the resulting expression, cf. (105) below. Moreover, from (90) we see that for tractions  we obtain
we obtain  .
.
Hence, we replace the saddle-point problem by

where

A stationary point of  is defined by the relations
is defined by the relations



and this system of equations takes the explicit form: For given values \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}, \bar {p}\), find the subscale fields  that solve the system
that solve the system



Finally, we obtain the macroscale energy density as

From the RVE-problem in (107), \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) is obtained directly as a primary variable. The volumetric strain \(\bar {e}\) is obtained by post-processing:

Remark.
The VMCM in (64) is still valid for the restricted space  . Since
. Since  , (64a) is valid for all
, (64a) is valid for all  .
.
Macroscale tangent relations
In order to solve the (generally nonlinear) macroscale problem (37) in the FE2-setting using Newton iterations, we need the pertinent tangent operators. Linearizing the implicit relations \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\) and \(\bar {e}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\) we obtain
thereby defining the tangents \(\bar {\textbf {\textsf {E}}}\) (4th order), \(\bar {\boldsymbol {E}}\) (2nd order), \(\bar {\boldsymbol {C}}\) (2nd order), and \(\bar {C}\) (scalar). Since a potential exists, it follows that \(\bar {\textbf {\textsf {E}}}\) possesses major symmetry and that \(\bar {\boldsymbol {E}} = \bar {\boldsymbol {C}}\), cf. Öhman et al. [14].
In order to compute the tangent operators, it is necessary to first compute the relevant sensitivity fields w.r.t. changes of the macroscale variables \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\bar {p}\), and they are solved from the pertinent tangent problem. On should then note that the particular sensitivity fields that are actually exploited (and needed) and the corresponding explicit formulation of the tangent problem depend on the chosen formulation of the RVE-problem (in terms of the boundary conditions: Weakly Periodic, Dirichlet, Neumann). Here, we shall give details only on the “generic” choice of the weakly periodic conditions.
Remark.
In the case of macroscale incompressibility, \(\bar {\boldsymbol {C}}\) and \(\bar {C}\) will vanish.
As a point of departure for computing the tangent tensors, we note that \(\bar {e}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\) is a primary variable in the RVE-problem, whereas \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\) is post-processed via (90). We thus need to compute sensitivities of \(\bar {e}\) and t from the tangent problem. To begin with, we establish the linearized form of (71) at the solution state to obtain




which must be valid for any given perturbations \(\mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\mathrm {d}\bar {p}\) giving rize to the corresponding perturbations du, dp, dt, and \(\mathrm {d}\bar {e}\) in the solution fields.
Next, we introduce orthonormal base dyads G i , i=1,2,…,8 to ensure that the deviatoric tensors ε d and σ d are, indeed, deviatoric in character. In other words we do not use the conventional base dyads e i ⊗e j , i,j=1,2,3, but we rather introduce the new set of base dyads such that the requirement G i :I=0 for i=1,2,…,8 is fulfilled. Examples of such (generally unsymmetric) dyads with Cartesian components, are
with respect to this basis, we have the representation
Next, we express the pertinent sensitivities via the representations
We thus obtain the following sets of tangent problems:
-
\(\mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}} = \boldsymbol {G}_{k}\) while \(\mathrm {d}\bar {p} = 0\): For k=1,…,8, solve for the sensitivities \(\boldsymbol {u}_{\mathrm {d}}^{(k)}\), \(p_{\mathrm {d}}^{(k)}\), \(\boldsymbol {t}_{\mathrm {d}}^{(k)}\), \(\bar {e}_{\mathrm {d}}^{(k)}\) from the system
 ((116a))
((116a))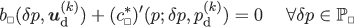 ((116b))
((116b)) ((116c))
((116c))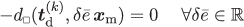 ((116d))
((116d)) -
\(\mathrm {d}\bar {p} = 1\) while \(\mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}} = \boldsymbol {0}\): Solve for the sensitivities u p, p p, t p, \(\bar {e}_{\mathrm {p}}\) from the system
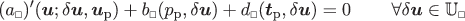 ((117a))
((117a))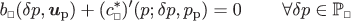 ((117b))
((117b)) ((117c))
((117c)) ((117d))
((117d))
Now, upon linearizing (90) and using the representation for dt in (115c), we obtain


Directly from (115d), we obtain
Macroscale tangent relations for the Dirichlet and Neumann boundary conditions are detailed in Appendix ‘Sensitivity problem’.
Bounds on the macroscale energy density
Since we have derived the Dirichlet and Neumann problems by respectively restricting the solution spaces as

it follows from (93), (102), and (84) that

In other words, the Dirichlet and Neumann boundary conditions represent upper and lower bounds on the macroscale energy density that is obtained with periodic boundary conditions for any given realization of the RVE and for a given macroscale state \((\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}, \bar {p})\). We note that choosing any discretization of  in (84) leads to a lower bound of \(\bar {\psi }\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\).
in (84) leads to a lower bound of \(\bar {\psi }\{{\bar {\boldsymbol {\epsilon }}}_{\mathrm {d}}, \bar {p}\}\).
In the case of linear elasticity, the tangent operators represent the upscaled (=homogenized) constant operators in the representations
whereby we obtain

Results and discussion
Preliminaries
Computations were carried out for a random composite with spherical particles embedded in a matrix, whereby both constituents are assumed to be homogeneous and isotropic linear elastic. The intrinsic properties are thus defined by the free energy expressions
where G and C (=K −1) are the shear stiffness and bulk compliance respectively. This choice corresponds to the standard relations \(\hat {\boldsymbol {\sigma }}_{\mathrm {d}}(\boldsymbol {\epsilon }_{\mathrm {d}}) = 2 G\,\boldsymbol {\epsilon }_{\mathrm {d}}\) and \(\hat {e}(p) = -C\, p\). The parameter set associated with the matrix and particles are (G mat,C mat) and (G part,C part), respectively.
All computational results were obtained for cubic Statistical Volume Elements (SVEs). The target volume fraction of (non-overlapping, spherical particles) if 10% and their size-distribution, in terms of diameter, is uniform in the range \(\left [\frac {2}{3},\frac {4}{3}\right ]\), thus with a mean value of 1. Two examples of realizations with SVE-size  and
and  are shown in Figure 4 and Figure 5, respectively.
are shown in Figure 4 and Figure 5, respectively.
Now, for sufficiently large size of the SVE (for any given realization of a random composite), we may assume that the macroscale response is isotropic corresponding to the effective moduli \(\bar {G}\) and \(\bar {C}\) (\(=\bar {K}^{-1}\)). However, even for a smaller SVE-size, it is possible to compute an “apparent” value of \(\bar {G}\) by the minimization
where I d is the deviatoric fourth order identity tensor such that the isotropic part of \(\bar {\textbf {\textsf {E}}}\) can be expressed as \(\bar {\textbf {\textsf {E}}}_{\text {iso}} = 2 \bar {G} \textbf {\textsf {I}}_{\mathrm {d}}\) in standard fashion.
For the finite element analysis of the SVE-problems, tetrahedral elements with so-called Mini-element approximations are utilized. This type of element is defined by linear approximation plus a bubble function for u and linear approximation for p, cf. [19].
The RVE‐problems with the different boundary conditions are implemented in the open source C++ code OOFEM (www.oofem.org) [20] and are available under the name MixedGradientPressure. However, due to the difficulty of constructing  , the present implementation of the weakly periodic boundary conditions is based on global polynomials for discretizing
, the present implementation of the weakly periodic boundary conditions is based on global polynomials for discretizing  . Thus, only a lower bound for the true periodicity is obtained. Due to the high computational cost, only the Neumann and Dirichlet boundary conditions are used in the numerical examples in this paper.
. Thus, only a lower bound for the true periodicity is obtained. Due to the high computational cost, only the Neumann and Dirichlet boundary conditions are used in the numerical examples in this paper.
Homogenization of macroscopically incompressible response — A convergence study
The first series of SVE-computations were carried out for macroscopically incompressible response, which is obtained when both matrix and particles are completely incompressible. Taking the shear modulus for the matrix, G
mat, as the reference modulus, we choose G
part=5 G
mat, whereas C
mat=C
part=0. Convergence results for the two extremes of Dirichlet and Neumann boundary conditions are shown in Figure 6. The mean value and variance of the homogenized shear modulus \(\bar {G}\) are shown for increasing SVE-size, represented by  . Here, a certain number of realizations are used for each value of
. Here, a certain number of realizations are used for each value of  , starting with 200 realizations for the smallest SVE size
, starting with 200 realizations for the smallest SVE size  and ending up with only 4 realizations for the largest SVE-size
and ending up with only 4 realizations for the largest SVE-size  that has approximately 500 thousand degrees of freedom. The Salome platform was used for generating the SVEs and the decrease of the number of realizations was due to the meshing code failing when inclusions badly intersect the boundary, which becomes increasingly likely with increasing
that has approximately 500 thousand degrees of freedom. The Salome platform was used for generating the SVEs and the decrease of the number of realizations was due to the meshing code failing when inclusions badly intersect the boundary, which becomes increasingly likely with increasing  . However, as seen in Figure 6, the variance is small in the homogenized results for
. However, as seen in Figure 6, the variance is small in the homogenized results for  and the mean values are still accurate. An RVE is obtained when the variance goes to zero, and the mean value converges, which is the case when the SVE-size is sufficiently large. In the present case, for engineering purposes, we consider
and the mean values are still accurate. An RVE is obtained when the variance goes to zero, and the mean value converges, which is the case when the SVE-size is sufficiently large. In the present case, for engineering purposes, we consider  sufficiently large to qualify as an RVE.
sufficiently large to qualify as an RVE.
Seamless transition from macroscopically compressible to incompressible response
In the second series of computations, we show how the homogenization scheme can seamlessly handle the transition from the macroscopically compressible to the incompressible response. Here, it is assumed that incompressible particles, defined by G
part=5 G
mat and C
part=0 (as before), are embedded in a matrix material with C
mat≥0. Only the situation with Dirichlet boundary conditions is considered (without affecting the generality of the main conclusion from the results). In Figure 7 it is shown how the homogenized properties are affected by the matrix compliance, C
mat, for a given (fixed) realization and given SVE-size  , cf. Figure 5), thus defining an RVE. Clearly, rather than choosing C
mat as the variable material property, one may choose Poisson’s ratio ν
mat via the elementary relation
, cf. Figure 5), thus defining an RVE. Clearly, rather than choosing C
mat as the variable material property, one may choose Poisson’s ratio ν
mat via the elementary relation
which is also used in Figure 7.
The computational results verify that the homogenization framework is able to handle the transition from macroscale compressibility to incompressibility when C mat→0 in a seamless fashion without any algorithmic changes. That macroscopical incompressibility is verified by the computed value \(\bar {C} = 0\). It is also noted in Figure 7 that the affect on \(\bar {G}\) is more pronounced, however quite limited, when incompressibility is approached.
Conclusions
In this paper we have introduced a variationally consistent homogenization scheme for heterogeneous solids, whose constituents may be incompressible in the extreme case. The mixed control of the homogenized quantities, \((\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}, \bar {p}) \to (\bar {\boldsymbol {\sigma }}_{\mathrm {d}}, \bar {e})\), is what enables the macroscopically incompressible response, whereas traditional strain-controlled homogenization, \(\bar {\boldsymbol {\epsilon }} \to \bar {\boldsymbol {\sigma }}\), leads to a singular problem when applied to fully incompressible microstructures. The transition from macroscopically compressible to incompressible states (which is the extreme result when all constituents are incompressible) is handled in a completely seamless fashion. Based on a mixed formulation on the fine scale, it has been demonstrated how the concept of variationally consistent homogenization can be adopted to derive the pertinent two-scale problem. The proposed canonical formulation of the problem on an underlying Representative Volume Element (RVE) is an extension of the formulation presented in Öhman et al. (2013), allowing for a general choice of boundary conditions. Moreover, the canonical formulation has been shown to satisfy the generalized macrohomogeneity condition. The FE-setting on both scales (macroscale and RVE) is based on the standard (u,p)-formulation, and the Mini-element approximation with a bubble function is adopted for the RVE-problem. All implementation and numerical results pertain to 3D-cubes.
It was shown that theoretical bounds on the “homogenized energy density” for weakly periodic boundary conditions on the RVE are obtained by imposing Dirichlet and Neumann boundary conditions. The computational results from a statistical analysis verify the convergence of these bounds with increasing SVE-size. As to the computational cost of solving the RVE-problem with the different types of boundary conditions for the standard compressible problem and the present (in)compressible one, it is concluded that the Neumann boundary condition is quite cost-neutral. However, applying the Dirichlet boundary condition to the canonical RVE-format means a noticeable additional cost, since the additional (global) variable \(\bar {e}\) is required in order to account for the (possibly vanishing) macroscale volumetric deformation. In this context, we remark that imposing weak periodicity would infer a further increased computational cost associated with the boundary discretization of tractions in  ; hence, it is conjectured that exploiting the standard Dirichlet and Neumann conditions computations and drawing conclusions about their bounding character would be a most competitive approach in FE2-computations.
; hence, it is conjectured that exploiting the standard Dirichlet and Neumann conditions computations and drawing conclusions about their bounding character would be a most competitive approach in FE2-computations.
As to future developments, it is desirable to further exploit the concept of weakly periodic boundary conditions; however, constructing basis functions for  in 3D is not a trivial task. Of course, it is also of interest to compare with the classical condition of strongly periodic fluctuations, which is defined by replacing (92) with
in 3D is not a trivial task. Of course, it is also of interest to compare with the classical condition of strongly periodic fluctuations, which is defined by replacing (92) with

and performing the corresponding steps up to (98). However, this method has the definite drawback that the meshing software must produce strictly periodic meshes.
In a forthcoming paper, the proposed theoretical framework will be applied to the problem of sintering, a characteristic of which is that the microstructure evolves from being highly porous to becoming completely dense. The “compaction” process is driven by surface tension along the particle-pores boundaries until the pore have completely disappeared, cf. Öhman et al. (2013).
Endnotes
a * indicates “complementary energy”
b Curly brackets {(∙)} indicate implicit and/or nonlocal functional dependence on (∙).
c Double arguments, i.e. \(\boldsymbol {u}(\bar {\boldsymbol {x}},\boldsymbol {x})\), are used to explicitly point out the underlying scale separation.
d
 , the “effective energy density”, for sufficiently large RVE.
, the “effective energy density”, for sufficiently large RVE.
Appendix
Variationally Consistent Homogenization (VCH)
VMS-approach – Scale separation and homogenization
Classical model-based homogenization can be formulated in the spirit of the Variational MultiScale method (VMS), cf. [21,22]. We introduce the abbreviated notation \(z = (\boldsymbol {u}, p) \in \mathbb {Z} = \mathbb {U} \times \mathbb {P}\), where  represents the space of fine-scale (non-homogenized) solutions to the system (3), which may conveniently be abbreviated in abstract form as the residual equatione
represents the space of fine-scale (non-homogenized) solutions to the system (3), which may conveniently be abbreviated in abstract form as the residual equatione
where \(\mathbb {Z}^{0} = \mathbb {U}^{0} \times \mathbb {P}\) is the test space and where each \(\boldsymbol {u}\in \mathbb {U}^{0}\) vanishes on the Dirichlet part of Γ.
A multiscale formulation of (129) is defined by the hierarchical split \(\mathbb {Z} = \mathbb {Z}^{\mathrm {M}} \oplus \mathbb {Z}^{\mathrm {s}}\), where \(\mathbb {Z}^{\mathrm {M}}\) contains smooth macroscale functions and \(\mathbb {Z}^{\mathrm {s}}\) is the hierarchical complement of \(\mathbb {Z}^{\mathrm {M}}\) that, typically, represents the fine-scale features. It is assumed that each \(z\in \mathbb {Z}\) can be split uniquely as z=z M+z s such that \(z^{\mathrm {M}} \in \mathbb {Z}^{\mathrm {M}}\) and \(z^{\mathrm {s}} \in \mathbb {Z}^{\mathrm {s}}\). Therefore, solve \(z^{\mathrm {M}} \in \mathbb {Z}^{\mathrm {M}}\), \(z^{\mathrm {s}} \in \mathbb {Z}^{\mathrm {s}}\) such that (129) can be represented by the set of equations
Without introducing further assumptions (approximations), the dimension of the original problem has not changed, i.e. (130) represent two global problems whose solution requires the same computational effort as does (129). In order to reduce the problem dimension based on homogenization (via the assumption of scale separation), we introduce the following key assumptions:
-
The integrands in the pertinent volume integrals are replaced by a running volume average on RVE’s of the type introduced in (11) such that, typically, the residual in (130a) can be rewritten in terms of the contributions defined on each RVE as
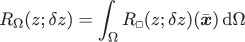 ((131))
((131))where
 is the RVE-residual that is localized to the Representative Volume Element (RVE). In practice (in FE-analysis), quadrature is used such that the evaluation of
is the RVE-residual that is localized to the Representative Volume Element (RVE). In practice (in FE-analysis), quadrature is used such that the evaluation of  is carried out only in the Gauss points.
is carried out only in the Gauss points.Furthermore, for the sake of simplicity we assume smoothness of boundary terms, such that R Γ (z;δ z M)≈R Γ (z M;δ z M), i.e. no boundary homogenization is necessary.
-
Local approximations for the fluctuation field z s are introduced in the spirit of VMS. This means that
 is the approximate solutionf of the fine-scale equation (130b) for given z
M, i.e. (130b) is replaced by “closed” RVE-problems (in the macroscale quadrature points) associated with a particular choice of boundary conditions on
is the approximate solutionf of the fine-scale equation (130b) for given z
M, i.e. (130b) is replaced by “closed” RVE-problems (in the macroscale quadrature points) associated with a particular choice of boundary conditions on  . In this paper we obtain such “closed” RVE-problems by choosing weakly periodic boundary conditions.
. In this paper we obtain such “closed” RVE-problems by choosing weakly periodic boundary conditions.
Returning to (130a), we now replace this problem by the approximate, homogenized, problem

which has the same dimension as (130a). We note that (132) represents a valid homogenization problem for any given choice of  ; however, to preserve typical Galerkin properties, such as symmetry of the macroscale tangent operator when such symmetry is inherent in the underlying fine-scale problem, it is crucial to satisfy the VCMC.
; however, to preserve typical Galerkin properties, such as symmetry of the macroscale tangent operator when such symmetry is inherent in the underlying fine-scale problem, it is crucial to satisfy the VCMC.
Variationally Consistent Macrohomogeneity Condition (VCMC)
We shall assume that there exists a potential Π(z) such that (132) represents the stationary point of Π(z), i.e. it is assumed that
Next, we introduce the crucial approximation (restriction) \(z \approx z^{\mathrm {M}} + \tilde {z}^{\mathrm {s}}\{z^{\mathrm {M}}\}\) before evaluation of the stationarity conditions, whereby we obtain
where \((\tilde {z}^{\mathrm {s}})'\{z^{\mathrm {M}};\delta z^{\mathrm {M}}\}\) denotes the sensitivity (or directional derivative) of \(\tilde z^{\mathrm {s}}\) for a variation δ z M of the macroscale solution z M. Hence, the choice of test function in (134) is restricted as compared to (133), and this restriction represents a “generalized Galerkin property” in terms of the underlying macroscale functions in \(\mathbb {Z}^{\mathrm {M}}\). Moreover, and most importantly, (134) is completely equivalent to the homogenized problem (132) if it is possible, for any given \(z^{\mathrm {M}}\in \mathbb {Z}^{\mathrm {M}}\), to satisfy the constraint
or, equivalently,
where the test space \(\tilde {\mathbb {Z}}'^{\mathrm {s}}(z^{\mathrm {M}})\), which is the tangent space to the approximation space, is defined as
Hence, any \(\mathrm {d} \tilde {z}^{\mathrm {s}}\in \tilde {\mathbb {Z}}'^{\mathrm {s}}(z^{\mathrm {M}})\) is a sensitivity of the fluctuation field \(\tilde {z}^{\mathrm {s}}\) for a differential change of the macroscale field z M within the considered RVE. It is computed from the tangent problem that is associated with the RVE-problem. We refer to (135) or (136) as a “Variationally Consistent (generalized) Macrohomogeneity Condition” (VCMC). Obviously, a sufficient condition for these identities to hold true is to require the RVE-residual to vanish on each RVE (in each quadrature point), i.e. to ensure that

An even stronger condition is to require that  for any
δ
z
s in a given set of functions that is defined locally for the considered RVE without requiring any implicit (or explicit) coupling to the sensitivity field \((\tilde {z}^{\mathrm {s}})'\{z^{\mathrm {M}};\delta z^{\mathrm {M}}\}\), which obviously defines a restricted choice of test functions. In such a case, the VCMC can be identified as precisely the classical Hill-Mandel macrohomogeneity condition.
for any
δ
z
s in a given set of functions that is defined locally for the considered RVE without requiring any implicit (or explicit) coupling to the sensitivity field \((\tilde {z}^{\mathrm {s}})'\{z^{\mathrm {M}};\delta z^{\mathrm {M}}\}\), which obviously defines a restricted choice of test functions. In such a case, the VCMC can be identified as precisely the classical Hill-Mandel macrohomogeneity condition.
Finally, we remark that the VCMC ensures that the macroscale tangent operator becomes symmetrical, since it holds that
With the introduced approximation \(z^{\mathrm {s}} \approx \tilde {z}^{\mathrm {s}}\{z^{\mathrm {M}}\}\), the test functions in (139) are chosen as
Homogenized macroscale energy
In order to show that  serves as the “macroscale energy density” for \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\), expressed by the relations (89), we first recall the identity
serves as the “macroscale energy density” for \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\) and \(\bar {e}\), expressed by the relations (89), we first recall the identity

where the RVE-potential  was defined in (83). Working out the total differential w.r.t. \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\bar {p}\) at equilibrium, we obtain
was defined in (83). Working out the total differential w.r.t. \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\bar {p}\) at equilibrium, we obtain

where we introduced the sensitivities w.r.t. changes in \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\bar {p}\) as follows:




Combining these with the (85), we can see that the last four terms in (142) vanish, i.e. . What remains of the total differential is thus
. What remains of the total differential is thus

Now, we may use (85a) and choose \(\delta \boldsymbol {u} = \mathrm {d}\bar {\boldsymbol {\epsilon }}\cdot [\!\boldsymbol {x} - \bar {\boldsymbol {x}}]\) to obtain

Finally, combining this result with (147), we obtain

which proves (89).
Sensitivity problem
Dirichlet boundary condition
Using the perturbations \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}} + \mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\bar {p} + \mathrm {d}\bar {p}\) in the linearized form of (98) at equilibrium we obtain



which must hold for any given \(\mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\mathrm {d}\bar {p}\). We thus consider the cases:
-
\(\mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}} = \boldsymbol {G}_{k}\) while \(\mathrm {d}\bar {p} = 0\) (with \(\boldsymbol {u}^{{\mathrm {M}}(k)}_{\mathrm {d}} \overset {\text {def}}{=} \boldsymbol {G}_{k} \cdot [\!\boldsymbol {x} - \bar {\boldsymbol {x}}]\)): For k=1,…,8, solve for the sensitivities \(\boldsymbol {u}_{\mathrm {d}}^{\mathrm {s}(k)}\), \(p_{\mathrm {d}}^{(k)}\), \(\bar {e}_{\mathrm {d}}^{(k)}\) from the system
 ((151a))
((151a))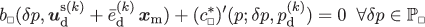 ((151b))
((151b)) ((151c))
((151c)) -
\(\mathrm {d}\bar {p} = 1\) while \(\mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}} = \boldsymbol {0}\): Solve for the sensitivities \(\boldsymbol {u}_{\mathrm {p}}^{\mathrm {s}}\), p p, \(\bar {e}_{\mathrm {p}}\) from the system
 ((152a))
((152a))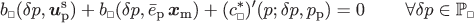 ((152b))
((152b))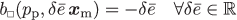 ((152c))
((152c))
Upon using the identity  , we deduce the tangent operators from
, we deduce the tangent operators from

Tangent operators associated with \(\bar {e}\) are obtained directly from the sensitivity analysis
Neumann boundary condition
Using the perturbations \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}} + \mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\bar {p} + \mathrm {d}\bar {p}\) in the linearized form of (107) at equilibrium we obtain



which must hold for any given \(\bar {\boldsymbol {\epsilon }}_{\mathrm {d}}\) and \(\mathrm {d}\bar {p}\). We thus consider the cases:
-
\(\mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}} = \boldsymbol {G}_{k}\) while \(\mathrm {d}\bar {p} = 0\): For k=1,…,8, solve for the sensitivities \(\boldsymbol {u}_{\mathrm {d}}^{(k)}\), \(p_{\mathrm {d}}^{(k)}\), \(\bar {\boldsymbol {\sigma }}_{\mathrm {d},\mathrm {d}}^{(k)}\) from the system
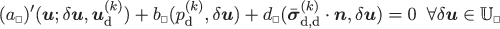 ((156a))
((156a))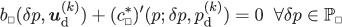 ((156b))
((156b)) ((156c))
((156c)) -
\(\mathrm {d}\bar {p} = 1\) while \(\mathrm {d}\bar {\boldsymbol {\epsilon }}_{\mathrm {d}} = \boldsymbol {0}\): Solve for the sensitivities u p, p p, \(\bar {\boldsymbol {\sigma }}_{\mathrm {d},\mathrm {p}}\) from the system
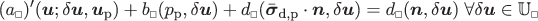 ((157a))
((157a)) ((157b))
((157b)) ((157c))
((157c))
Directly from the solution we obtain tangent operators associated with \(\bar {\boldsymbol {\sigma }}_{\mathrm {d}}\):
For tangent operators associated with \(\bar {e}\), we obtain

Abbreviations
- RVE:
-
Representative volume element
- SVE:
-
Statistical volume element
- VCH:
-
Variationally consistent homogenization
- VMS:
-
Variational multiScale
- VCMC:
-
Variationally consistent macrohomogeneity condition
References
Torquato S (2006) Random heterogeneous materials: microstructure and macroscopic properties. Springer. ISBN: 0387951679.
Zohdi TI, Wriggers P (2004) An introduction to computational micromechanics. Lecture notes in applied and computational mechanics. ISBN: 978-3-540-77482-2.
Fish J (2013) Practical multiscaling. Wiley. ISBN: 978-1-118-41068-4. http://eu.wiley.com/WileyCDA/WileyTitle/productCd-1118410688.html Accessed 2014-02-28.
Geers MGD, Kouznetsova VG, Brekelmans WAM (2010) Multi-scale computational homogenization: trends and challenges. J Comput Appl Math 234(7): 2175–2182. doi:10.1016/j.cam.2009.08.077.
Coenen EWC, Kouznetsova VG, Geers MGD (2011) Enabling microstructure-based damage and localization analyses and upscaling. Model Simulat Mater Sci Eng 19(7): 074008. doi:10.1088/0965-0393/19/7/074008. Accessed 2014-09-09.
Coenen EWC, Kouznetsova VG, Geers MGD (2012) Novel boundary conditions for strain localization analyses in microstructural volume elements. Int J Numer Meth Eng 90(1): 1–21. doi:10.1002/nme.3298. Accessed 2014-09-09.
Temizer İ, Wu T, Wriggers P (2013) On the optimality of the window method in computational homogenization. Int J Eng Sci 64: 66–73. doi:10.1016/j.ijengsci.2012.12.007. Accessed 2014-02-26.
Larsson F, Runesson K, Saroukhani S, Vafadari R (2011) Computational homogenization based on a weak format of micro-periodicity for RVE-problems. Comput Meth Appl Mech Eng 200(1–4): 11–26. doi:10.1016/j.cma.2010.06.023.
Coenen EWC, Kouznetsova VG, Geers MGD (2012) Multi-scale continuous-discontinuous framework for computational-homogenization-localization. J Mech Phys Solid 60(8): 1486–1507. doi:10.1016/j.jmps.2012.04.002. Accessed 2014-02-26.
Aragón AM, Soghrati S, Geubelle PH (2013) Effect of in-plane deformation on the cohesive failure of heterogeneous adhesives. J Mech Phys Solid 61(7): 1600–1611. doi:10.1016/j.jmps.2013.03.003. Accessed 2014-09-09.
McBride A, Mergheim J, Javili A, Steinmann P, Bargmann S (2012) Micro-to-macro transitions for heterogeneous material layers accounting for in-plane stretch. J Mech Phys Solid 60(6): 1221–1239. doi:10.1016/j.jmps.2012.01.003. Accessed 2014-02-26.
Larsson R, Landervik M (2013) A stress-resultant shell theory based on multiscale homogenization. Comput Meth Appl Mech Eng 263: 1–11. doi:10.1016/j.cma.2013.04.011. Accessed 2014-02-28.
Sandström C, Larsson F (2013) Variationally consistent homogenization of stokes flow in porous media. Int J Multiscale Comput Eng 11: 117–138. doi:10.1615/IntJMultCompEng.2012004069.
Öhman M, Runesson K, Larsson F (2012) Computational mesoscale modeling and homogenization of liquid-phase sintering of particle agglomerates. Technische Mechanik 32: 463–483.
Olevsky EA (1998) Theory of sintering: from discrete to continuum. Materials Science and Engineering: R: Reports 23(2): 41–100. doi:10.1016/S0927-796X(98)00009-6. Accessed 2014-02-26.
Guo Z, Peng X, Moran B (2007) Large deformation response of a hyperelastic fibre reinforced composite: Theoretical model and numerical validation. Compos Appl Sci Manuf 38(8): 1842–1851. doi:10.1016/j.compositesa.2007.04.004. Accessed 2014-09-09.
Öhman M, Runesson K, Larsson F (2013) Computational homogenization of liquid-phase sintering with seamless transition from macroscopic compressibility to incompressibility. Comput Meth Appl Mech Eng 266: 219–228. doi:10.1016/j.cma.2013.07.006.
Larsson F, Runesson K, Su F (2010) Variationally consistent computational homogenization of transient heat flow. Int J Numer Meth Eng 81(13): 1659–1686. doi:10.1002/nme.2747.
Arnold DN, Brezzi F, Fortin M (1984) A stable finite element for the stokes equations. Calcolo 21(4): 337–344.
Patzák B, Bittnar Z (2001) Design of object oriented finite element code. Adv Eng Software 32(10–11): 759–767. doi:10.1016/S0965-9978(01)00027-8.
Hughes TJR, Feijo GR, Mazzei L, Quincy J-B (1998) The variational multiscale method - a paradigm for computational mechanics. Comput Meth Appl Mech Eng 166(1–2): 3–24. doi:10.1016/S0045-7825(98)00079-6.
Larson MG, Målqvist A (2007) Adaptive variational multiscale methods based on a posteriori error estimation: Energy norm estimates for elliptic problems. Comput Meth Appl Mech Eng 196(21–24): 2313–2324. doi:10.1016/j.cma.2006.08.019.
Acknowledgements
The work was funded by the Swedish Research Council.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The theory represents joint work by all authors. MÖ developed the computer code for the numerical simulations. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Öhman, M., Runesson, K. & Larsson, F. On the variationally consistent computational homogenization of elasticity in the incompressible limit. Adv. Model. and Simul. in Eng. Sci. 2, 1 (2015). https://doi.org/10.1186/s40323-014-0017-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40323-014-0017-1




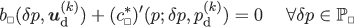

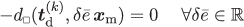
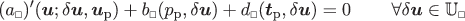
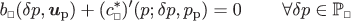






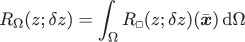
 is the RVE-residual that is localized to the Representative Volume Element (RVE). In practice (in FE-analysis), quadrature is used such that the evaluation of
is the RVE-residual that is localized to the Representative Volume Element (RVE). In practice (in FE-analysis), quadrature is used such that the evaluation of  is the approximate solutionf of the fine-scale equation (
is the approximate solutionf of the fine-scale equation (